
Evaluating Probabilistic Forecasters with sktime and tsbootstrap — Easy-to-Use, Configurable Frameworks for Reproducible Science
Abstract¶
Evaluating probabilistic forecasts is complex and essential across various domains, yet no comprehensive software framework exists to simplify this task. Despite extensive literature on evaluation methodologies, current practices are fragmented and often lack reproducibility. To address this gap, we introduce a reproducible experimental workflow for evaluating probabilistic forecasting algorithms using the sktime package. Our framework features a unified software API for forecasting algorithms, a simple specification language for complex algorithms, including meta-algorithms like bootstrapping, probabilistic performance metrics, and standardized evaluation workflows. We demonstrate the framework’s efficacy through a study evaluating prediction intervals added to point forecasts. Our results highlight the improved prediction accuracy and reliability of combined approaches. We provide reusable code and invite contributions from the research community to extend our experiments and tackle computational challenges for broader studies.
1Introduction¶
Making probabilistic forecasts is challenging, and evaluating probabilistic forecasts, or the algorithms that produce them, is even more difficult.
A significant body of literature focuses on developing robust meta-methodologies for evaluation. This includes evaluation metrics such as the Continuous Ranked Probability Score (CRPS) Gneiting & Katzfuss, 2014 and their properties, like properness, as well as benchmarking setups and competitions like the Makridakis competitions Makridakis et al., 2020Makridakis et al., 2022. This meta-field builds upon a broader primary field that develops methodologies for algorithms producing probabilistic forecasts, encompassing classical methods, uncertainty estimation techniques like bootstrap or conformal intervals, and modern deep learning and foundation models Chen et al., 2020Nowotarski & Weron, 2018Rasul et al., 2023Das et al., 2023.
Despite the critical importance of evaluating probabilistic forecasts in various domains, including finance, energy, healthcare, and climate science, no comprehensive software framework or interface design has emerged to cover all these needs with a simple workflow or specification language. For instance, the reproducing code for the Makridakis competitions—while extensive in scope—relies on forecasts generated from disparate software interfaces. Similar issues are found in other benchmarking studies, where code availability is often limited or nonexistent Semmelrock et al., 2023Király et al., 2018. This lack of unified interfaces makes it challenging for practitioners in both industry and academia to contribute to or verify the growing body of evidence.
To address these limitations, we present a simple, reproducible experimental workflow for evaluating probabilistic forecasting algorithms using sktime Király et al., 2024. As of 2024, the sktime package provides the most comprehensive collection of time series-related algorithms in unified interfaces and stands out as the only major, non-commercially governed framework for time series forecasting.
The key components of this reproducible benchmarking framework are:
A unified software API for forecasting algorithms, mirroring a unified mathematical interface.
Composite forecasters (meta-algorithms), such as adding prediction intervals via time series bootstrapping, which themselves follow the same forecasting interface from both software and mathematical perspectives.
A first-order language that allows for the unambiguous specification of even complex forecasting algorithms.
A unified software API for probabilistic performance metrics, covering metrics for distribution as well as interval or quantile forecasts.
A standardized workflow for obtaining benchmark result tables for combinations of algorithms, metrics, and experimental setups.
To demonstrate the efficacy and ease of use of sktime in benchmarking probabilistic forecasters, we conducted a small study exploring the performance of various meta-algorithms (wrappers) that add prediction intervals to point forecasters. We investigated a range of forecasters, including Naive Forecasting and AutoTheta models Spiliotis et al., 2020, along with probabilistic wrappers such as Conformal Intervals and BaggingForecaster with different bootstrapping methods. For the bootstrapping methods, we use the tsbootstrap library Gilda, 2024Gilda et al., 2024.
The study’s goal was to evaluate the effectiveness of these combined approaches in improving prediction accuracy and reliability.
We conducted experiments on several common datasets, including Australian electricity demand Godahewa et al., 2021, sunspot activity Godahewa et al., 2021, and US births Godahewa et al., 2021. These datasets represent different time frequencies and characteristics.
Our paper is accompanied by easily reusable code, and we invite the open research and open-source communities to contribute to extending our experiments or using our code to set up their own. As is often the case in modern data science, computational power is a limiting factor, so we hope to leverage the SciPy conference to plan a more comprehensive set of studies.
The remainder of this paper is organized as follows: In Section 3, we describe the forecasting methods and probabilistic wrappers used in our experiments. Section 4.2 provides an overview of the datasets used for evaluation. In Section 4.3, we present the experimental results and discuss the performance of the combined approaches. Finally, in Section 5, we conclude the paper and outline directions for future research.
2sktime and tsbootstrap for Reproducible Experiments¶
In this section, we summarize the key design principles used for reproducible benchmarking in sktime. Thereby, from a software perspective, it is worth noting that sktime Löning et al., 2019Király et al., 2024 contains multiple native implementations, including naive methods, all probability wrappers, and pipeline composition, but also provides a unified interface across multiple packages in the time series ecosystem, e.g.:
tsbootstrap Gilda, 2024Gilda et al., 2024: A library for time series bootstrapping methods, integrated with
sktime.statsforecast Federico Garza, 2022: A library for statistical and econometric forecasting methods, featuring the Auto-Theta algorithm.
statsmodels Perktold et al., 2024: A foundational library for statistical methods, used for the deseasonalizer and various statistical primitives.
This hybrid use of sktime as a framework covering first-party (itself), second-party (tsbootstrap), and third-party (statsmodels, statsforecast) packages is significant. Credit goes to the maintainers and implementers of these packages for implementing the contained algorithms that we can interface.
2.1Unified Interface¶
In sktime and tsbootstrap, algorithms and mathematical objects are treated as first-class citizens. All objects of the same type, such as forecasters, follow the same interface. This consistency ensures that every forecaster is exchangeable with any other. The same holds for all bootstrapping methods in tsbootstrap. Thus, they are easily exchangeable enabling simple and fast experimentation.
Forecasters are objects with fit and predict methods, allowing both the target time series (endogenous data) and the time series that influence the target time series (exogenous data) to be passed. For example, the following code (Program 1) specifies a forecaster, fits it, and makes predictions.
# importing the necessary modules
from sktime.datasets import load_airline
from sktime.forecasting.naive import NaiveForecaster
# load exemplary data
y = load_airline()
# specifying the forecasting algorithm
forecaster = NaiveForecaster(strategy="last", sp=12)
# fitting the forecaster -- forecast y into the future, 3 steps ahead
forecaster.fit(y, fh=[1, 2, 3])
# querying predictions
y_pred = forecaster.predict()Program 1:Exemplary code for fitting and predicting with a forecaster
A crucial design element in the above is that line 9 can specify any forecaster - for instance, ARIMA or ExponentialSmoothing, and the rest of the code will work without modification.
Currently, sktime supports the construction of 82 individual forecasters. Some of these are implemented directly in sktime, but sktime also provides adapters providing a unified API to forecasting routines from other libraries, such as gluonts and prophet. Each forecaster is parametric, with configurations ranging from 1 to 47 parameters across different forecasters. A list of forecasters can be obtained or filtered via the all_estimators utility.
from sktime.registry import all_estimators
# get all forecasters
all_forecasters = all_estimators("forecaster")
# get all forecasters that support prediction intervals
all_estimators("forecaster", filter_tags={"capability:pred_int": True})Program 2:Code to list all forecaster and all probabilistic forecasters (tag=capability:pred_int)
To better filter the forecasters (as well as the other estimators such as classifiers and regressors) based on their properties and capabilities and to control their behaviour, sktime implements a tag system. Each estimator, such as a forecaster, has a dict _tags, with a string as a key describing the name and a value of an arbitrary type describing the property. This type system enables an easy identification of all probabilistic forecasters, since they are tagged with the "capability:pred_int" tag. Currently, 45 of the 82 forecasters support probabilistic prediction modes (Program 2), such as prediction intervals, quantile predictions, or full distributional predictions:
# importing the necessary modules
from sktime.datasets import load_airline
from sktime.forecasting.naive import NaiveForecaster
# load exemplary data
y = load_airline()
# specifying the forecasting algorithm
forecaster = NaiveForecaster(strategy="last", sp=12)
# fitting the forecaster -- forecast y into the future, 3 steps ahead
forecaster.fit(y, fh=[1, 2, 3])
# making interval predictions
y_pred_int = forecaster.predict_interval()
# making distribution predictions
y_pred_proba = forecaster.predict_proba()Program 3:Exemplary probabilistic forecast with NaiveForecaster
More details can be found in the official tutorials (an overview of notebooks and tutorials is provided on our homepage). Creating algorithms with compatible APIs is straightforward.
sktime and tsbootstrap provide fill-in extension templates for creating algorithms in a compatible interface, which can be shared in a third-party code base and indexed by sktime, or contributed directly to sktime.
2.2Reproducible Specification Language¶
All objects in sktime are uniquely specified by their construction string, which serves as a reproducible blueprint. Algorithms are intended to be stable and uniquely referenced across versions; full replicability can be achieved by freezing Python environment versions and setting random seeds.
For example, the specification string NaiveForecaster(strategy="last", sp=12) uniquely specifies a native implementation of the seasonal last-value-carried-forecaster, with seasonality parameter 12.
Typical sktime code specifies the forecaster as Python code, but it can also be used as a string to store or share specifications. The registry.craft utility converts a Python string into an sktime object, ensuring easy reproducibility:
from sktime.registry import craft
forecaster = craft('NaiveForecaster(strategy="last", sp=12)')Code to craft a forecaster from a string
which can be used to copy a full specification from a research paper and immediately construct the respective algorithm in a Python environment, even if full code has not been shared by the author.
This approach makes it extremely easy to share specifications reproducibly, simplifying the often convoluted process of describing algorithms in research papers.
2.3Meta-Algorithms and Composability¶
sktime provides not only simple algorithms as objects in unified interfaces but also meta-algorithms, such as data processing pipelines or algorithms that add interval forecast capability to existing forecasting algorithms. Importantly, these composites also follow unified interfaces.
This leads to a compositional specification language with rich combinatorial flexibility. For example, the following code adds conformal prediction interval estimates to the NaiveForecaster (Program 5):
# importing the necessary modules
from sktime.datasets import load_airline
from sktime.forecasting.naive import NaiveForecaster
from sktime.forecasting.conformal import ConformalIntervals
# load exemplary data
y = load_airline()
# specifying the forecasting algorithm
forecaster = ConformalIntervals(NaiveForecaster(strategy="last", sp=12))
# fitting the forecaster -- forecast y into the future, 3 steps ahead
forecaster.fit(y, fh=[1, 2, 3])
# making interval predictions
y_pred_int = forecaster.predict_interval()Program 5:Code to add conformal prediction intervals to a forecaster
The conformal prediction interval fits multiple instances of the wrapped forecaster on parts of the time series using window sliding. In particular, each forecaster’s instance is fit on the time series , where . Afterwards, the residuals are computed on the remaining time series , where is the length of the time series. Out of these residuals, the prediction intervals are computed. The resulting algorithm possesses fit, predict, and - added by the wrapper - predict_interval, as well as the capability:pred_int tag.
Data transformation pipelines can be constructed similarly, or with an operator-based specification syntax (Program 6):
# importing the necessary modules
from sktime.datasets import load_airline
from sktime.forecasting.naive import NaiveForecaster
from sktime.transformations.series.detrend import Deseasonalizer
from sktime.transformations.series.difference import Differencer
# load exemplary data
y = load_airline()
pipeline = Differencer() * Deseasonalizer(sp=12) * NaiveForecaster(strategy="last")
# fitting the forecaster -- forecast y into the future, 3 steps ahead
pipeline.fit(y, fh=[1, 2, 3])
# making interval predictions
y_pred_int = pipeline.predict()Program 6:Code to construct a pipeline with a differencer and a seasonalizer
This creates a forecasting algorithm that first computes differences, then remove the seasonality (deseasonalize) by assuming a periodicity of 12. Then the NaiveForecaster(strategy="last") uses the last value as prediction for the next value (last-value-carry-forward method). Finally it adds the seasonality back and inverts the first differences. As before, the resulting forecaster provides unified interface points and is interchangeable with other forecasters in sktime.
2.4Probabilistic Metrics¶
In sktime, evaluation metrics are first-class citizens. Probabilistic metrics compare the ground truth time series with predictions, representing probabilistic objects such as predictive intervals or distributions. For example:
# importing the necessary modules
from sktime.datasets import load_airline
from sktime.forecasting.naive import NaiveForecaster
from sktime.performance_metrics.forecasting.probabilistic import CRPS
from sktime.split import temporal_train_test_split
# load exemplary data
y = load_airline()
y_train, y_test = temporal_train_test_split(y, test_size=36)
# specifying the forecasting algorithm
forecaster = NaiveForecaster(strategy="last", sp=12)
# fitting the forecaster -- forecast y into the future, 3 steps ahead
forecaster.fit(y_train, fh=y_test.index)
# making interval predictions
y_pred_int = forecaster.predict_interval()
# making distribution predictions
y_pred_proba = forecaster.predict_proba()
# Initialise the CRPS metric
crps = CRPS()
# Calculate the CRPS
crps(y_test, y_pred_proba)Program 7:Code to make probabilistic forecasts and calculate the CRPS
Tags control the type of probabilistic prediction expected, such as "scitype:y_pred" with the value "pred_proba" for CRPS.
2.5Benchmarking and Evaluation¶
Our benchmarking framework involves a standardized workflow for obtaining benchmark result tables for combinations of algorithms, metrics, and experimental setups. Here is an example of how to add forecasters and tasks:
# Example code to add forecasters and tasks
# Import the necessary modules
from sktime.benchmarking.forecasting import ForecastingBenchmark
from sktime.datasets import load_airline
from sktime.forecasting.naive import NaiveForecaster
from sktime.performance_metrics.forecasting.probabilistic import CRPS
from sktime.split import SlidingWindowSplitter
# Initialise the benchmark object
benchmark = ForecastingBenchmark()
# Add a forecaster to the benchmark
benchmark.add_estimator(
estimator=NaiveForecaster(strategy="last", sp=12),
estimator_id="naive_forecaster"
)
# Initialise the Splitter
cv_splitter = SlidingWindowSplitter(
step_length=12,
window_length=24,
fh=range(12)
)
# Add a task to the benchmark
# A task is a combination of a dataset loader, a splitter, and a list of metrics
benchmark.add_task(
load_airline,
cv_splitter,
[CRPS()]
)
# Run the benchmark
benchmark.run("result.csv")Program 8:Example usage of the ForecastingBenchmark in sktime.
This approach ensures that our benchmarking process is both comprehensive and reproducible.
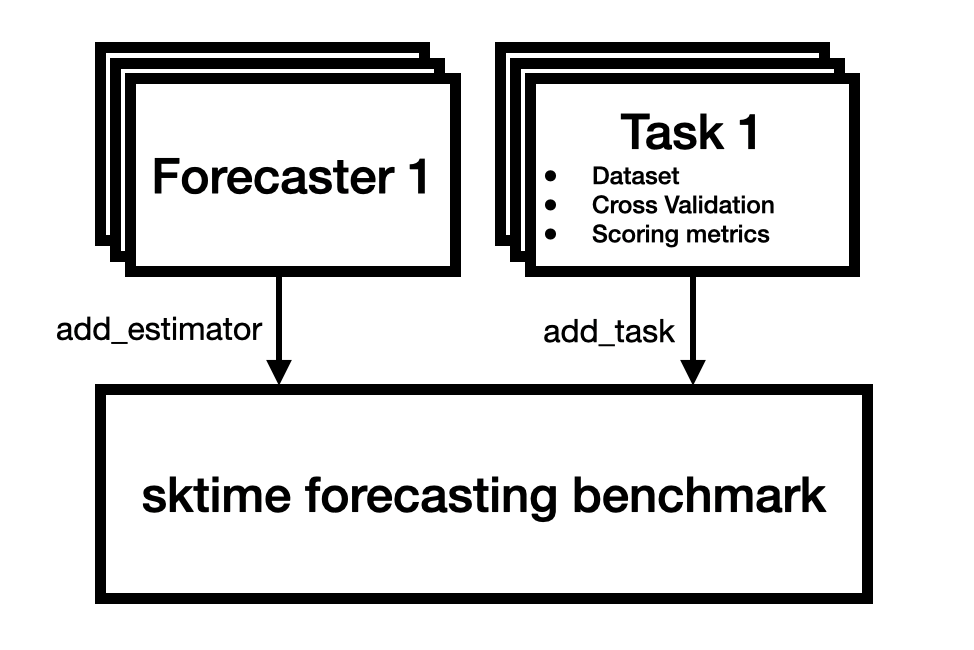
Figure 1:Benchmarking and evaluation framework
2.6Prior Work¶
The design principles of sktime draw inspiration from several established machine learning frameworks. Notably, scikit-learn in Python Pedregosa et al., 2011, mlr in R Bischl et al., 2016, and Weka Hall et al., 2009 have pioneered the use of first-order specification languages and object-oriented design patterns for machine learning algorithms.
sktime extends these foundational ideas by introducing specialized interfaces for time series forecasting, including both point and probabilistic forecasts. It also incorporates unique features such as:
Probabilistic forecasters and associated metrics interfaces
Reproducibility patterns and APIs
Meta-algorithms for enhanced composability
Inhomogeneous API composition for flexible algorithmic design
Additionally, the R/fable package O'Hara-Wild et al., 2024 has contributed similar concepts specifically tailored to forecasting, which sktime has expanded upon or adapted to fit within its framework.
By leveraging and building upon these prior works, sktime offers a comprehensive and adaptable toolkit for time series forecasting, fostering reproducible research and facilitating extensive benchmarking and evaluation. For a detailed analysis of design patterns in AI framework packages and innovations in sktime, see Király et al., 2021.
3Algorithmic Setup¶
In this section, we describe the forecasting algorithms used in our experiments. Our methods combine traditional forecasting models with uncertainty estimation wrappers, showcasing the benchmarking and model specification capabilities of sktime. This study serves as an invitation to the scientific Python community to engage and contribute to a more systematic study with reproducible specifications.
3.1Forecasting Pipeline¶
Each forecaster is wrapped in a Differencer and a Deseasonalizer as preprocessing steps to improve stationarity. These preprocessors are necessary because some forecasters require the time series to be stationary (i.e., the properties of the time series at time , , ..., do not depend on the observation at time Hyndman & Athanasopoulos, 2018) and non-seasonal.
Differencer: Computes first differences, which are inverted after forecasting by cumulative summing.Deseasonalizer(sp=data_sp): Removes the seasonal component, which is added back after forecasting. It estimates the trend by applying a convolution filter to the data, removing the trend, and then averaging the de-trended series for each period to return the seasonal component.
All used forecasters are point forecasters, i.e., for each time step they provide one value (point), and no information about the uncertainty of the forecast. Thus, they are combined with one of the probabilistic wrappers to generate prediction intervals or quantile forecasts.
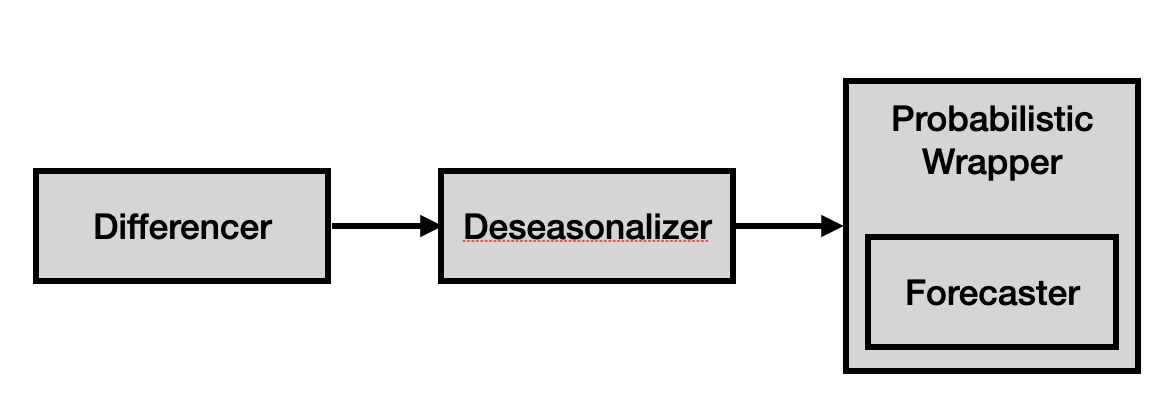
Figure 2:The forecasting pipeline used for all the forecasters
The partial pipeline specification, illustrated in Figure 2, is:
Differencer() * Deseasonalizer(sp=data_sp) * wrapper(forecaster)where variable parts are wrapper, forecaster, and data_sp. These components are varied as described below. Note the code for running the whole benchmark is provided in the Section 4.
3.2Component Forecasting Models¶
We use several component forecasting models in this study, each with unique characteristics:
NaiveForecaster(strategy, sp): Uses simple heuristics for forecasting. Thestrategyparameter allows selecting the type of algorithm:mean: Uses the mean of the last values, with seasonal periodicityspif passed.last: Uses the last observed, with seasonal periodicityspif passed.drift: Fits a line between the first and last values of the considered window and extrapolates forward.
StatsForecastAutoTheta(sp): A variant of the Theta model of Assimakopoulos & Nikolopoulos (2000) with automated parameter tuning, from thestatsforecastlibrary.
3.3Probabilistic Wrappers¶
We use the following probabilistic wrappers to enhance the forecasting models:
ConformalIntervals(forecaster, strategy): Uses conformal prediction methods Shafer & Vovk (2008) to produce non-parametric prediction intervals. Variants of the method are selected by thestrategyparameter: Empirical and Empirical Residual use training quantiles, with the latter using symmetrized residuals. Conformal implements the method of Shafer & Vovk (2008), and Conformal Bonferroni applies the Bonferroni correction Sedgwick, 2012 .BaggingForecaster(bootstrap_transformer, forecaster): Provides probabilistic forecasts by bootstrapping time series and aggregating the bootstrap forecasts Hyndman & Athanasopoulos, 2018Bergmeir et al., 2016. TheBaggingForecastertakes a bootstrap algorithmbootstrap_transformer, a first-class object insktime. Various bootstrap algorithms with their parameters are applied in the study.NaiveVariance(forecaster): Uses a sliding window to compute backtesting residuals, aggregated by forecasting horizon to a variance estimate. The mean is obtained from the wrapped forecaster, and variance from the pooled backtesting estimate.SquaringResiduals(forecaster, residual_forecaster): Uses backtesting residuals on the training set, squares them, and fits theresidual_forecasterto the squared residuals. Forecasts ofresidual_forecasterare used as variance predictions, with mean predictions fromforecaster, to obtain a normal distributed forecast. In this study,residual_forecasteris alwaysNaiveForecaster(strategy="last").
3.4Bootstrapping Techniques¶
Bootstrapping methods generate multiple resampled datasets from the original time series data, which can be used as part of wrappers to estimate prediction intervals or predictive distributions. In this study, we use bootstrap algorithms from tsbootstrap Gilda et al., 2024Gilda, 2024, sktime Király et al., 2024, and scikit-learn Pedregosa et al., 2011 compatible framework library dedicated to time series bootstrap algorithms. sktime adapts these algorithms via the TSBootstrapAdapter, used as bootstrap_transformer in BaggingForecaster.
MovingBlockBootstrap: Divides the time series data into overlapping blocks of a fixed size and resamples these blocks to create new datasets. The block size is chosen to capture the dependence structure in the data.BlockDistributionBootstrap: Generates bootstrapped samples by fitting a distribution to the residuals of a model and then generating new residuals from the fitted distribution. This method assumes that the residuals follow a specific distribution, such as Gaussian or Poisson, and handles dependencies by resampling blocks of residuals. To create a new time series, the bootstrapped residuals are added to the model’s fitted values.BlockResidualBootstrap: Designed for time series data where a model is fit to the data, and the residuals (the difference between the observed and predicted data) are bootstrapped. This method is particularly useful when a good model fit is available for the data. The bootstrapped samples are created by adding the bootstrapped residuals to the model’s fitted values.BlockStatisticPreservingBootstrap: Generates bootstrapped time series data while preserving a specific statistic of the original data. This method handles dependencies by resampling blocks of data while ensuring that the preserved statistic remains consistent.
In this study, these bootstrapping techniques are used to estimate the distribution of forecasts and generate robust prediction intervals and predictive distributions as part of the BaggingForecaster.
3.5Evaluation Metrics¶
We evaluate the performance of our forecasting models using the following metrics:
CRPS- Continuous Ranked Probability Score Matheson & Winkler, 1976 measures the accuracy of probabilistic forecasts by comparing the predicted distribution to the observed values. The CRPS for a real-valued forecast distribution and an observation can be defined as:where and are independent random variables with distribution .
PinballLoss- the pinball loss, also known as quantile loss Steinwart & Christmann, 2011, evaluates the accuracy of quantile forecasts by penalizing deviations from the true values based on specified quantiles. For quantile forecasts at levels and an observation , the Pinball Loss is defined as:The experiment uses the Pinball Loss at quantiles 0.05, and 0.95.
AUCalibration- The Area between the calibration curve and the diagonal assesses how well the prediction intervals capture the true values. For observations and corresponding distributional predictions with quantile functions (where for the cdf ), the AUCalibration is defined as:where and is the -th order statistic of .
IntervalWidth- width of prediction intervals, or sharpness measures the concentration of the prediction intervals. More concentrated intervals indicate higher confidence in the forecasts. Sharpness is desirable because it indicates precise predictions. Sharpness is calculated as the average width of the prediction intervals.EmpiricalCoverage- Empirical coverage measures how much of the observations are within the predicted interval. It is computed as the proportion of observations that fall within the prediction, providing a direct measure of the reliability of the intervals. A prediction interval ranging from the 5th to the 95th quantile should cover 90% of the observations. I.e., the empirical coverage should be close to 0.9.runtime- Besides metrics that assess the quality of the forecast, average runtime for an individual fit/interence run is also reported. Runtime measures the computational efficiency of the forecasting methods, which is crucial for practical applications.
4Experiments¶
In this section, we describe the experimental setup, the datasets, the evaluation metrics, and the experimental procedures. We explain how the experiments are designed to compare the performance of different forecasting methods.
4.1Experimental Setup¶
To perform the benchmarking study, we use the framework described in Section 3. The benchmarking compares different probabilistic wrappers on different datasets and with different forecasters regarding CRPS, Pinball Loss, AUCalibration, and Runtime.
To enable easy replication of the experiments, we provide for each used forecaster, and wrapper the hyperparameters by providing the used Python object instantiation in Table 1. Note, that the parameter seasonal periodicity (sp) is dataset dependent and is set to 48 for the Australian Electricity Dataset and 1 for the other datasets.
To create the cross validation folds, we use the SlidingWindowSplitter from sktime. The instantiation of the splitter for each dataset is shown in Table 3. Figure 3 is showing the resulting cross validation folds for the tree datasets. The properties of the datasets are summarized in Table 2.
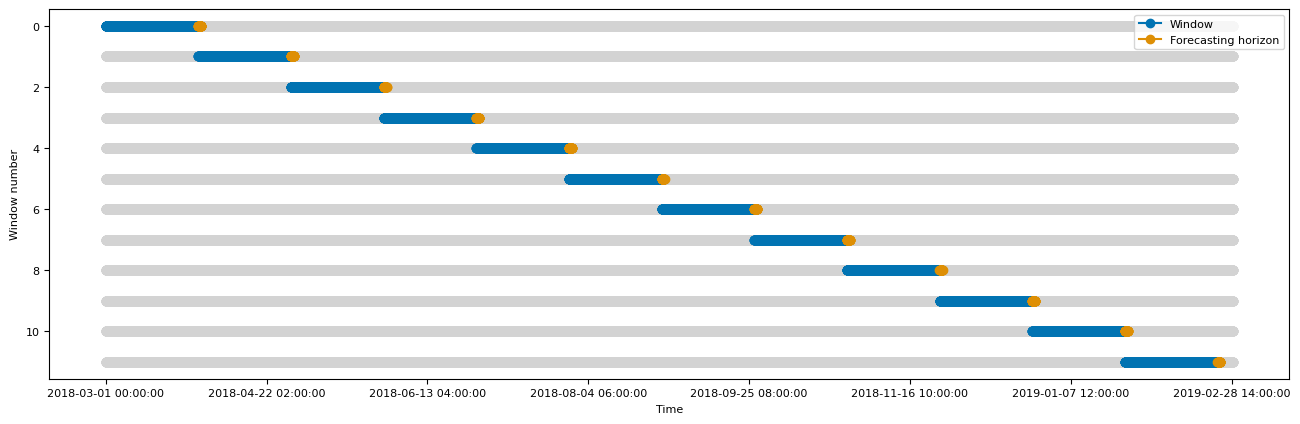
(a)Australian Electricity Demand
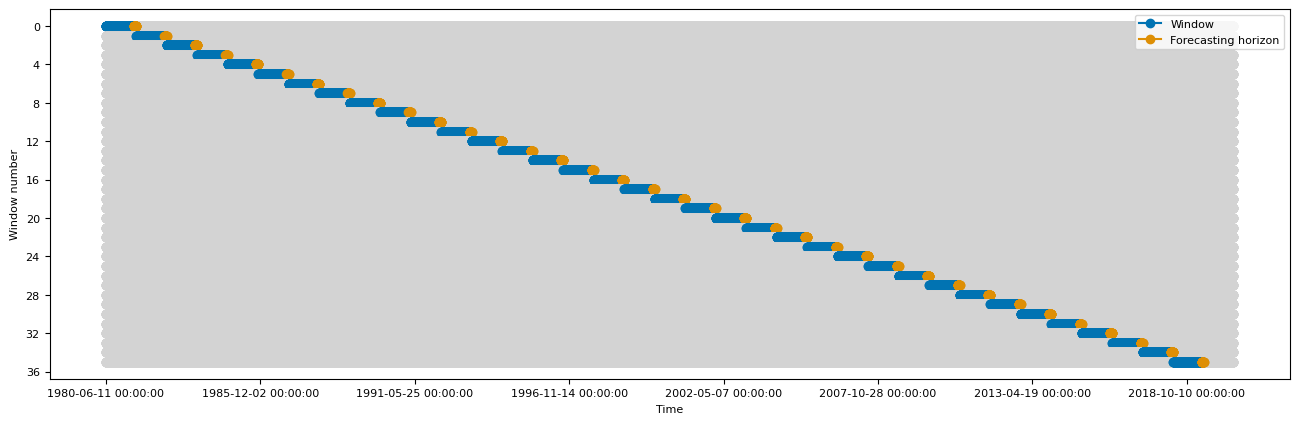
(b)Sunspot Activity
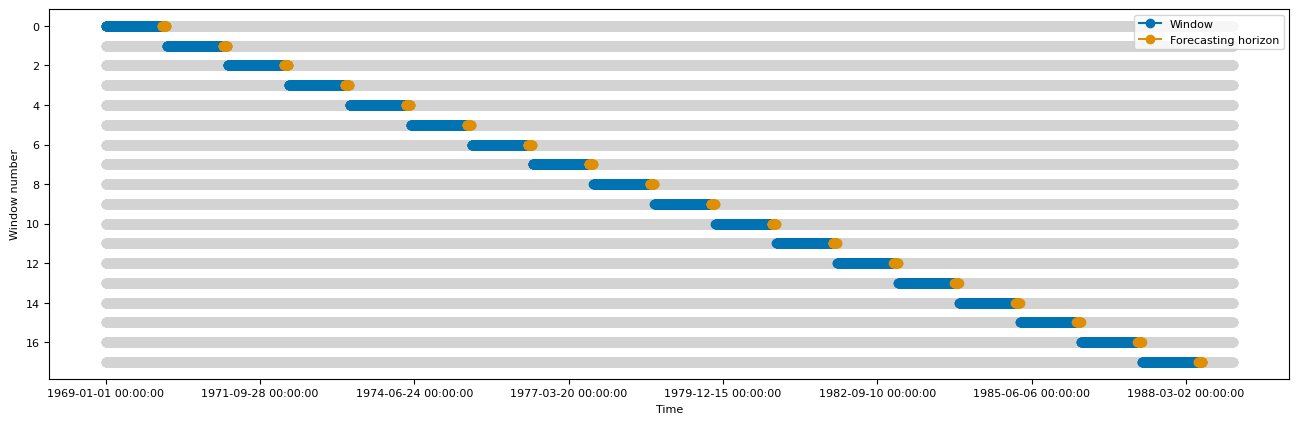
(c)US Births
Figure 3:The splits used for the evaluation on the three datasets. Blue indicates the training data, and orange indicates the test data. The splits are created using the parameters from Table 2 and Table 3
4.2Datasets¶
We evaluate our forecasting methods and probabilistic wrappers on several diverse time series datasets, each offering unique characteristics:
Australian Electricity Demand Godahewa et al., 2021: Half-hourly electricity demand data for five states of Australia: Victoria, New South Wales, Queensland, Tasmania, and South Australia, useful for high-frequency data evaluation.
Sunspot Activity Godahewa et al., 2021: Weekly observations of sunspot numbers, ideal for testing forecasting robustness on long-term periodic patterns.
US Births Godahewa et al., 2021: Daily birth records in the United States, with a clear seasonal pattern, suitable for daily data performance assessment.
Table 1:The table lists the specification strings for the estimators used in the study. Note that a full pipeline consists of pre-processing, wrapper, and base forecaster, as detailed in Section 3.
Some of the parameters are determined by the used dataset: sp is 48 for the Autralian Electricity Dataset and 1 for the other. The sample_freq is 0.005 for the Australian Electricity Dataset and 0.1 for the other.
| Role | Name | Hyperparameters |
| Base Forecaster | Naive last | NaiveForecaster(strategy="last", sp=sp) |
| Base Forecaster | Naive mean | NaiveForecaster(strategy="mean", sp=sp) |
| Base Forecaster | Naive drift | NaiveForecaster(strategy="drift", sp=sp) |
| Base Forecaster | Theta | StatsForecastAutoTheta(season_length=sp) |
| Wrapper | CI Empirical | ConformalIntervals(forecaster, sample_frac=sample_frac) |
| Wrapper | CI Empirical residuals | ConformalIntervals(forecaster, sample_frac=sample_frac, method="empirical_residual") |
| Wrapper | CI Conformal | ConformalIntervals(forecaster, sample_frac=sample_frac, method="conformal") |
| Wrapper | CI Bonferroni | ConformalIntervals(forecaster, sample_frac=sample_frac, method="conformal_bonferroni") |
| Wrapper | BaggingForecaster | BaggingForecaster(ts_bootstrap_adapter, forecaster)) |
| Wrapper | Naive Variance | NaiveVariance(forecaster, initial_window=14*sp)) |
| Wrapper | Squaring Residuals | SquaringResiduals(forecaster, initial_window=14*sp)) |
| Forecasting Pipeline | Pipeline | Differencer(1) * Deaseasonalizer(sp=sp) * Wrapper |
| ts_bootstrap_adapter | TSBootstrapAdapter | TSBootstrapAdapter(tsbootsrap) |
| tsbootstrap | Moving Block Bootstrap | MovingBlockBootstrap() |
| tsbootstrap | Block Residual Bootstrap | BlockDistributionBootstrap() |
| tsbootstrap | Block Statistic Preserving Bootstrap | BlockStatisticPreservingBootstrap() |
| tsbootstrap | Block Distribution Bootstrap | BlockDistributionBootstrap() |
Table 2:To perform the evaluation, we used three datasets. Due to the different frequencies and lengths, we used different parameters for the Sliding Window Splitter to create the cross-validation folds. This table presents the parameters used for each dataset.
| Dataset | Forecast Horizon | Step Width | Window Size | Cutout Period | Number of Folds | Seasonal Periodicity |
| Australian Electricity Demand | 48 | 1440 | 1440 | Last Year | 12 | 48 |
| Sunspot Activity | 28 | 395 | 365 | Last 40 Years | 12 | 1 |
| US Births | 28 | 395 | 365 | Whole Time Series | 12 | 1 |
Table 3:The code instantiation of the cross-validation splits used for the evaluation on the three datasets. The parameters are taken from Table 2.
| Dataset | CV splitter |
| Australian Electricity Demand | SlidingWindowSplitter(step_length=48*30, window_length=48*30,fh=range(48)) |
| Sunspot Activity | SlidingWindowSplitter(step_length=395, window_length=365,fh=range(28)) |
| US Births | SlidingWindowSplitter(step_length=395, window_length=365,fh=range(28)) |
4.3Results¶
In this section, we present the results of our experiments. We evaluate the performance of the forecasting methods combined with probabilistic wrappers on the datasets described in Section 4.2.
To increase the conciseness, we calculated the rank of each probabilistic wrapper for each combination of forecaster, metric, and dataset. Afterwards, for each metric, probabilistic wrapper and dataset, we have calculated the average across all forecasters and time series. In the following, we present the results for each dataset separately, except for the runtime, which is the same for all three experiments. Thus, we describe it only for the Australian Electricity Demand dataset.
4.3.1Performance on Australian Electricity Demand¶
The results for the Australian electricity demand dataset are summarized in Table 4. We compare the performance of different forecasting models and probabilistic wrappers using the previously described evaluation metrics.
The ranked based evaluation show that diverse results regarding the different metrics. E.g. while CI Empirical Residual performs best on CRPS, it is only mediocre regarding the Pinball Loss and the AUCalibration. On PinballLoss, the best method is CI Empirical and on AUCalibration, it is Moving Block Bootstrap. Regarding the runtime, the fastest method is the fallback probabilistic prediction of the base forecaster. The slowest methods are NaiveVariance and SquaringResiduals. Furthermore, it seems that the ConformalIntervals are slightly faster than the BaggingForecasters.
Table 4:Performance of forecasting methods on the Australian electricity demand dataset
| Wrapper | CRPS | Pinball Loss | AUCalibration | Runtime |
| Fallback | 9.45 | 9.66 | 5.61 | 1.00 |
| Naive Variance | 7.75 | 7.20 | 7.15 | 10.00 |
| Squaring Residuals | 7.45 | 6.20 | 5.05 | 11.00 |
| Block Distribution Bootstrap | 4.08 | 3.15 | 6.82 | 7.83 |
| Block Residual Bootstrap | 4.30 | 5.58 | 5.84 | 8.32 |
| Block Statistic Preserving Bootstrap | 4.25 | 5.87 | 6.15 | 7.29 |
| Moving Block Bootstrap | 6.12 | 6.51 | 4.26 | 6.00 |
| CI Conformal | 5.75 | 5.40 | 5.69 | 3.92 |
| CI Empirical | 3.79 | 2.63 | 6.97 | 3.30 |
| CI Empirical Residual | 2.37 | 5.42 | 5.35 | 3.49 |
| CI Bonferroni | 10.50 | 8.05 | 6.70 | 3.70 |
4.3.2Performance on Sunspot Activity¶
Table 5 shows the performance of our methods on the sunspot activity dataset. The long-term periodic patterns in this dataset provide a challenging test for our forecasting models.
The ranked based evaluation show that BaggingForecaster with the Block Distribution Bootstrap scores clearly best regarding the CRPS and Pinball Loss, and AUCalibration.
Table 5:Performance of forecasting methods on the sunspot activity dataset
| Wrapper | CRPS | PinballLoss | AUCalibration | Runtime |
| Fallback | 9.00 | 7.25 | 9.50 | 1.00 |
| Naive Variance | 6.50 | 6.25 | 7.75 | 10.00 |
| Squaring Residuals | 8.00 | 8.00 | 4.75 | 11.00 |
| Block Distribution Bootstrap | 1.00 | 1.00 | 3.00 | 7.25 |
| Block Residual Bootstrap | 6.00 | 6.25 | 5.00 | 6.75 |
| Block Statistic Preserving Bootstrap | 5.50 | 7.00 | 2.50 | 6.25 |
| Moving Block Bootstrap | 5.75 | 5.75 | 7.50 | 5.00 |
| CI Conformal | 4.75 | 4.50 | 6.75 | 4.50 |
| CI Empirical | 5.50 | 4.00 | 7.25 | 4.50 |
| CI Empirical Residual | 3.50 | 8.00 | 6.25 | 4.25 |
| CI Bonferroni | 10.50 | 8.00 | 5.75 | 5.50 |
4.3.3Performance on US Births¶
The results for the US births dataset are presented in Table 6. This dataset, with its clear seasonal pattern, allows us to assess the models’ ability to handle daily data. The ranked based evaluation show that BaggingForecaster with the Block Distribution Bootstrap scores best regarding the CRPS and Pinball Loss. Regarding the AUCalibration, the best score is achieved by CI Conformal.
Table 6:Performance of forecasting methods on the US births dataset
| Wrapper | CRPS | PinballLoss | AUCalibration | Runtime |
| Fallback | 9.25 | 9.50 | 7.88 | 1.00 |
| Naive Variance | 6.25 | 5.75 | 6.25 | 10.00 |
| Squaring Residuals | 9.50 | 8.50 | 6.50 | 11.00 |
| Block Distribution Bootstrap | 1.00 | 1.00 | 8.25 | 7.25 |
| Block Residual Bootstrap | 3.75 | 5.75 | 5.50 | 7.00 |
| Block Statistic Preserving Bootstrap | 5.50 | 6.00 | 7.38 | 6.25 |
| Moving Block Bootstrap | 5.75 | 5.25 | 5.12 | 4.75 |
| CI Conformal | 6.00 | 6.00 | 4.75 | 4.25 |
| CI Empirical | 5.50 | 4.50 | 4.88 | 4.75 |
| CI Empirical Residual | 3.00 | 6.00 | 5.00 | 5.25 |
| CI Bonferroni | 10.50 | 7.75 | 4.50 | 4.50 |
5Discussion and Conclusion¶
Our experiments demonstrate that the benchmarking framework in sktime provides an easy-to-use solution for reproducible benchmarks. We showed this by conducting simple benchmark studies of probabilistic wrappers for point forecasts on three different systems and make the corresponding code available at: https://
Regarding our benchmark study, we note that this is a limited study primarily aimed at showcasing the capabilities of the proposed framework. Therefore, future work should include a comprehensive hyperparameter search to identify the best parameters for the probabilistic wrappers. Additionally, further bootstrapping methods need to be explored, as well as other wrappers such as generative neural networks, including Generative Adversarial Networks, Variational Autoencoders, or Invertible Neural Networks Phipps et al., 2024Wang et al., 2020.
Besides extending the range of wrappers, we also plan to include additional point forecasters as base models, such as AutoARIMA, in our study. Furthermore, the number of examined datasets should be expanded to provide a more comprehensive evaluation. Finally, we did not perform a grid search on the hyperparameters for the wrappers, which means that with different hyperparameters, their performance and runtime might change.
In conclusion, the sktime evaluation modules enable the performance of reproducible forecasting benchmarks. We demonstrated its applicability in a small benchmarking study that compares different probabilistic wrappers for point forecasters. In future work, we aim to collaborate with the scientific community to integrate more wrappers and conduct a broader benchmark study on this topic.
Copyright © 2024 Heidrich et al. This is an open-access article distributed under the terms of the Creative Commons Attribution 4.0 International license, which enables reusers to distribute, remix, adapt, and build upon the material in any medium or format, so long as attribution is given to the creators.
- AUC
- Area Under Calibration Curve
- CI
- Conformal Interval
- CRPS
- Continuous Ranked Probability Score
- Gneiting, T., & Katzfuss, M. (2014). Probabilistic forecasting. Annual Review of Statistics and Its Application, 1, 125–151. https://doi.org/10.1146/annurev-statistics-062713-085831
- Makridakis, S., Spiliotis, E., & Assimakopoulos, V. (2020). The M4 Competition: 100,000 time series and 61 forecasting methods. International Journal of Forecasting, 36(1), 54–74. https://doi.org/10.1016/j.ijforecast.2019.04.014
- Makridakis, S., Spiliotis, E., & Assimakopoulos, V. (2022). M5 accuracy competition: Results, findings, and conclusions. International Journal of Forecasting, 38(4), 1346–1364. https://doi.org/10.1016/j.ijforecast.2021.11.013
- Chen, Y., Kang, Y., Chen, Y., & Wang, Z. (2020). Probabilistic forecasting with temporal convolutional neural network. Neurocomputing, 399, 491–501. https://doi.org/10.1016/j.neucom.2020.03.011
- Nowotarski, J., & Weron, R. (2018). Recent advances in electricity price forecasting: A review of probabilistic forecasting. Renewable and Sustainable Energy Reviews, 81, 1548–1568. https://doi.org/10.1016/j.rser.2017.05.234
- Rasul, K., Ashok, A., Williams, A. R., Khorasani, A., Adamopoulos, G., Bhagwatkar, R., Biloš, M., Ghonia, H., Hassen, N. V., Schneider, A., & others. (2023). Lag-llama: Towards foundation models for time series forecasting. arXiv Preprint arXiv:2310.08278. https://doi.org/10.48550/arXiv.2310.08278
- Das, A., Kong, W., Sen, R., & Zhou, Y. (2023). A decoder-only foundation model for time-series forecasting. arXiv Preprint arXiv:2310.10688. https://doi.org/10.48550/arXiv.2310.10688
- Semmelrock, H., Kopeinik, S., Theiler, D., Ross-Hellauer, T., & Kowald, D. (2023). Reproducibility in Machine Learning-Driven Research. https://doi.org/10.48550/arXiv.2307.10320
- Király, F. J., Mateen, B., & Sonabend, R. (2018). NIPS - Not Even Wrong? A Systematic Review of Empirically Complete Demonstrations of Algorithmic Effectiveness in the Machine Learning and Artificial Intelligence Literature. https://doi.org/10.48550/arXiv.1812.07519
- Király, F., Löning, M., Bagnall, T., Middlehurst, M., Ganesh, S., Walter, M., Oastler, G., Lines, J., Ray, A., ViktorKaz, Mentel, L., Heidrich, B., Mishra, S., chrisholder, Bartling, D., Tsaprounis, L., RNKuhns, Gilbert, C., Baichoo, M., … Khrapov, S. (2024). sktime/sktime: v0.29.0 (v0.29.0) [Computer software]. Zenodo. 10.5281/zenodo.11095261
- Spiliotis, E., Assimakopoulos, V., & Makridakis, S. (2020). Generalizing the theta method for automatic forecasting. European Journal of Operational Research, 284(2), 550–558. https://doi.org/10.1016/j.ejor.2020.01.007
- Gilda, S. (2024). tsbootstrap. Zenodo. 10.5281/zenodo.10866090
- Gilda, S., Heidrich, B., & Kiraly, F. (2024). tsbootstrap: Enhancing Time Series Analysis with Advanced Bootstrapping Techniques. https://doi.org/10.48550/arXiv.2404.15227
- Godahewa, R., Bergmeir, C., Webb, G., Hyndman, R., & Montero-Manso, P. (2021). Australian Electricity Demand Dataset (Version 1) [Data set]. Zenodo. 10.5281/zenodo.4659727
- Godahewa, R., Bergmeir, C., Webb, G., Hyndman, R., & Montero-Manso, P. (2021). Sunspot Daily Dataset (without Missing Values) (Version 4) [Data set]. Zenodo. 10.5281/zenodo.4654722
