
A Modified Strassen Algorithm to Accelerate Numpy Large Matrix Multiplication with Integer Entries
Abstract¶
Numpy is a popular Python library widely used in the math and scientific community because of its speed and convenience. We present a Strassen type algorithm for multiplying large matrices with integer entries. The algorithm is the standard Strassen divide and conquer algorithm but it crosses over to Numpy when either the row or column dimension of one of the matrices drops below 128. The algorithm was tested on a MacBook, an I7 based Windows machine as well as a Linux machine running a Xeon processor and we found that for matrices with thousands of rows or columns and integer entries, the Strassen based algorithm with crossover performed 8 to 30 times faster than regular Numpy on such matrices. Although there is no apparent advantage for matrices with real entries, there are a number of applications for matrices with integer coefficients.
Introduction¶
A recent article Fink et al., 2021 suggests that Python is rapidly becoming the Lingua Franca of machine learning and scientific computing because of powerful frameworks such as Numpy, SciPy, and TensorFlow. These libraries offer great flexibility while boosting the performance of Python because they are written in compiled C and C++.
In this short paper we present a modified Strassen-based Strassen, 1969 algorithm for multiplying large matrices of arbitrary sizes containing integer entries. The algorithm uses Strassen’s algorithm for several divide and conquer steps before crossing over to a regular Numpy matrix multiplication. For large matrices the method is 8 to 30 times faster than calling Numpy.matmul or Numpy.dot to multiply the matrices directly. The method was tested on a variety of hardware and the speed advantage was consistent for cases with integer entries. There is no such advantage for matrices with floating point entries however as Harvey & Hoeven, 2018 points out, there are numerous applications for large matrices with integer entries, including high precision evaluation of so-called holonomic functions (e.g. exp, log, sin, Bessel functions, and hypergeometric functions) as well as areas of Algebraic Geometry to name just two. Integer matrices are also frequently used as adjacency matrices in graph theory applications and are also used extensively in combinatorics.
To give the reader some early perspective, we will see later in the paper that some of the matrix multiplies that we do with the suggested algorithm take approximately two minutes using the new algorithm, but take 44 minutes using Numpy.matmul.
It is suggested in Python.org, 2022 that Numpy may be the single most-imported non-stdlib module in the entire Pythonverse. Therefore, an algorithm that speeds Numpy for large integer matrices may be of interest to a large audience.
Motivating Exploration with Baseline Timings¶
For motivation consider the well-known standard algorithm for multiplying a pair of matrices, as found in GeeksforGeeks, 2022 as well as any algorithms book.
#multiply matrix A and B and put
#the product into C.
#A,B,C are assumed to be square
#matrices of the same dimension.
#No error checking is done.
def multiply(A, B, C):
for i in range(N):
for j in range( N):
C[i][j] = 0
for k in range(N):
C[i][j]+=A[i][k]*B[k][j]It is clear from the three nested loops that this algorithm has running time.
Strassen’s algorithm Strassen, 1969 is described most easily in Figure 1 which is modified from GeeksForGeeks GeeksforGeeks, 2022. We see that to multiply two matrices via Strassen’s method requires seven multiplications plus eighteen additions or subtractions of matrices that are size . The additions and subtractions will cost and therefore the time complexity of Strassen’s algorithm is which by the Master Theorem Cormen et al., 2009 is . Python code for an initial implementation of the standard Strassen algorithm can be found in GeeksforGeeks, 2022.
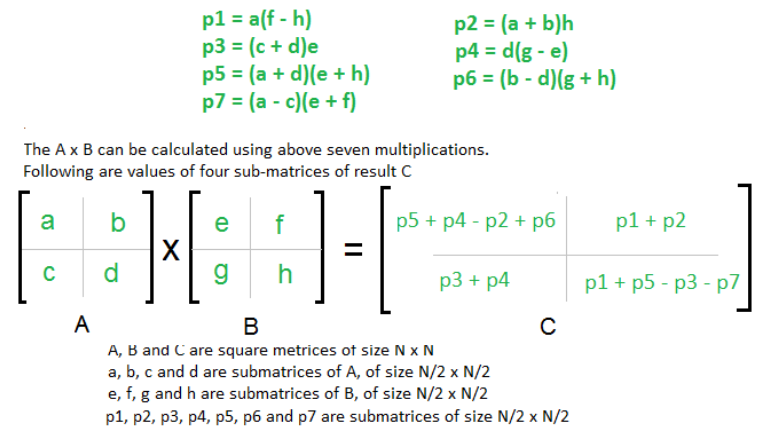
Figure 1:Illustration of Strassen’s Algorithm for multiplying 2 Square Matrices (Modified from GeeksForGeeks)
To get a baseline for our improved algorithms below we show how the standard multiplication and the Geeks-for-Geeks implementation of the Strassen algorithm perform compared to Numpy.matmul on several large square matrices with integer coefficients. Timings are provided in Table 1. Unsurprisingly, the Numpy implementation of matrix multiply is orders of magnitude faster than the other methods. This is expected because Numpy is written in compiled C and as discussed above is known for its speed and efficiency. The table contains a column where we compute the current timing divided by the previous timing. As noted above the complexity of Strassen’s algorithm is thus when we double the size of we expect the timing to increase about 7-fold. The current/previous column shows that this is the case. Similarly we expect the standard algorithm’s timing to increase about 8-fold when we double the and this seems to be the case as well. Still, the Strassen algorithm as implemented here is not a practical algorithm in spite of the lower complexity. Although it would start to be faster than the standard matrix multiplication for and larger, it would not rival the Numpy multiplication until reached 1016
Table 1:Timing for Base Algorithms on Matrices with Integer Entries. (Intel Core I7-9700 CPU @ 3.00 GHz, 8 Cores)
| Numpy | Strassen 1 | Standard Multiply | ||||
| Matrix Size | Time (seconds) | Current/ Previous | Time (seconds) | Current/ Previous | Time (seconds) | Current/ Previous |
| 128x128 | 0.002 | - | 3.777 | - | 1.869 | - |
| 256x256 | 0.02 | 8.728 | 26.389 | 6.986 | 15.031 | 8.043 |
| 512x512 | 0.222 | 10.999 | 188.781 | 7.154 | 125.279 | 8.334 |
Table 2:Timings (seconds) for Matrix Multiplication on Square Matrices with Integer Entries. MacBook Pro 16 with Core i7 @ 2.6 GHz
| Matrix Size | Numpy | Strassen | Strassen16 | Strassen32 | Strassen64 | Strassen128 | Strassen256 | Strassen512 | Standard |
| 128 x 128 | 0.00 | 3.88 | 0.02 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 1.32 |
| 256 x 256 | 0.03 | 26.85 | 0.13 | 0.03 | 0.01 | 0.01 | 0.01 | 0.01 | 10.67 |
| 512 x 512 | 0.27 | 188.09 | 0.90 | 0.19 | 0.09 | 0.08 | 0.11 | 0.20 | 86.63 |
| 1024 x 1024 | 3.75 | ——— | 6.70 | 1.41 | 0.64 | 0.63 | 0.82 | 1.45 | ——— |
| 2048 x 2048 | 82.06 | ——— | 44.03 | 9.29 | 4.24 | 4.23 | 5.44 | 9.84 | ——— |
| 4096 x 4096 | 988.12 | ——— | 322.82 | 68.06 | 31.61 | 31.10 | 40.14 | 72.56 | ——— |
| 8192 x 8192 | 14722.33 | ——— | 2160.77 | 457.28 | 211.77 | 211.02 | 270.69 | 483.54 | ——— |
Table 3:Timings (seconds) for Matrix Multiplication on Square Matrices with Integer Entries. MacBook Pro 16 with Core i7 @ 2.6 GHz
| Matrix Size | Numpy | Strassen | Strassen128 | Standard | ||||
| Time (s) | Current / Previous | Time (s) | Current / Previous | Time (s) | Current / Previous | Time (s) | Current / Previous | |
| 128 x 128 | 0.00 | 3.88 | 0.00 | 1.32 | ||||
| 256 x 256 | 0.03 | 11.30 | 26.85 | 6.93 | 0.01 | 7.39 | 10.67 | 8.07 |
| 512 x 512 | 0.27 | 10.20 | 188.09 | 7.00 | 0.08 | 7.48 | 86.63 | 8.12 |
| 1024 x 1024 | 3.75 | 13.69 | ——— | 0.63 | 7.72 | ——— | ||
| 2048 x 2048 | 82.06 | 21.89 | ——— | 4.23 | 6.67 | ——— | ||
| 4096 x 4096 | 988.12 | 12.04 | ——— | 31.10 | 7.35 | ——— | ||
| 8192 x 8192 | 14722.33 | 14.90 | ——— | 211.02 | 6.78 | ——— | ||
Table 4:Timings (seconds) for Matrix Multiplication on Square Matrices with Integer Entries. Windows 11 with Core i7 @ 3.0 GHz
| Matrix Size | Numpy | Strassen | Strassen128 | Standard | ||||
| Time (s) | Current / Previous | Time (s) | Current / Previous | Time (s) | Current / Previous | Time (s) | Current / Previous | |
| 128 x 128 | 0.00 | 3.76 | 0.00 | 1.96 | ||||
| 256 x 256 | 0.02 | 8.80 | 27.67 | 7.36 | 0.01 | 6.96 | 15.60 | 7.95 |
| 512 x 512 | 0.22 | 10.77 | 183.88 | 6.64 | 0.10 | 7.06 | 124.48 | 7.98 |
| 1024 x 1024 | 1.94 | 8.97 | 1283.43 | 6.98 | 0.68 | 7.03 | 1002.26 | 8.05 |
| 2048 x 2048 | 77.42 | 439.91 | 8979.96 | 7.00 | 4.84 | 7.07 | 8426.06 | 8.41 |
| 4096 x 4096 | 760.60 | 9.82 | 63210.78 | 7.04 | 35.40 | 7.31 | 68976.25 | 8.19 |
| 8192 x 8192 | 7121.69 | 9.36 | 441637.97 | 6.99 | 239.26 | 6.76 | 549939.81 | 7.97 |
Table 5:Timings (seconds) for Matrix Multiplication on Square Matrices with Integer Entries. Linux with Xeon E5-2680 v3 @ 2.50GHz
| Matrix Size | Numpy | Strassen | Strassen128 | Standard | ||||
| Time (s) | Current / Previous | Time (s) | Current / Previous | Time (s) | Current / Previous | Time (s) | Current / Previous | |
| 128 x 128 | 0.00 | 4.58 | 0.00 | 1.82 | ||||
| 256 x 256 | 0.03 | 9.56 | 32.71 | 7.14 | 0.02 | 7.91 | 15.11 | 8.29 |
| 512 x 512 | 0.45 | 17.77 | 228.34 | 6.98 | 0.11 | 6.76 | 122.98 | 8.14 |
| 1024 x 1024 | 4.21 | 9.38 | ——— | 0.78 | 7.26 | ——— | ||
| 2048 x 2048 | 98.00 | 23.27 | ——— | 5.61 | 7.21 | ——— | ||
| 4096 x 4096 | 1029.60 | 10.51 | ——— | 41.88 | 7.46 | ——— | ||
| 8192 x 8192 | 10050.31 | 9.76 | ——— | 287.43 | 6.86 | ——— | ||
Implementing Strassen with a Crossover to Numpy¶
It is clear from the initial timings in Table 1 that to improve the Strassen implementation we should crossover to Numpy at some level of our recursion rather than go all the way to the base case.
As long as we are modifying the algorithm we should also generalize it so that is will work on any size matrices. The current strassen function described in Figure 1 will crash if given a matrix with odd row dimension or odd column dimension. We can easily fix this by padding matrices with a row of zeros in the case of an odd row dimension or by padding with a column of zeros in the case of an odd column dimension. Code for padding a single row or column can be found below.
"""add row of zeros to bottom of matrix"""
def padRow(m):
x = []
for i in range(len(m[0])):
x.append(0)
return(np.vstack((m,x)))
def padColumn(m):
"""add column of zeros to right of matrix"""
x = []
for i in range(len(m)):
x.append(0)
return(np.hstack((m,np.vstack(x))))Since the padded rows (or columns) will need to be removed from the product at each level one might wonder whether padding once to a power of 2 would be more efficient? For example, a matrix with 17 rows and 17 columns will be padded to , but then each of its submatrices will be padded to which will require submatrices to be padded and so on. Cases like this could be avoided by padding the original matrix to . This was tested however, and it was found that padding of a single row at multiple levels of recursion is considerably faster than padding to the next power of 2.
To ensure that the new version of Strassen based matrix multiplier shown below works as expected, more than a million matrix multiplications of various sizes and random values were computed and compared to Numpy.matmul to ensure both gave the same answer.
#x,y, are matrices to be multiplied. crossoverCutoff
#is the dimension where recursion stops.
def strassenGeneral(x, y,crossoverCutoff):
#Base case when size <= crossoverCutoff
if len(x) <= crossoverCutoff:
return np.matmul(x,y)
if len(x[0])<= crossoverCutoff:
return np.matmul(x,y)
rowDim = len(x)
colDim = len(y[0])
#if odd row dimension then pad
if (rowDim & 1 and True):
x = padRow(x)
y = padColumn(y)
#if odd column dimension then pad
if (len(x[0]) & 1 and True):
x = padColumn(x)
y = padRow(y)
if (len(y[0]) & 1 and True):
y = padColumn(y)
#split the matrices into quadrants.
a, b, c, d = split(x)
e, f, g, h = split(y)
#Compute the 7 products, recursively (p1, p2...p7)
if (len(x) > crossoverCutoff):
p1 = strassenGeneral(a, f - h,crossoverCutoff)
p2 = strassenGeneral(a + b, h,crossoverCutoff)
p3 = strassenGeneral(c + d, e,crossoverCutoff)
p4 = strassenGeneral(d, g - e,crossoverCutoff)
p5 = strassenGeneral(a + d, e + h,crossoverCutoff)
p6 = strassenGeneral(b - d, g + h,crossoverCutoff)
p7 = strassenGeneral(a - c, e + f,crossoverCutoff)
else:
p1 = np.matmul(a, f - h)
p2 = np.matmul(a + b, h)
p3 = np.matmul(c + d, e)
p4 = np.matmul(d, g - e)
p5 = np.matmul(a + d, e + h)
p6 = np.matmul(b - d, g + h)
p7 = np.matmul(a - c, e + f)
#combine the 4 quadrants into a single matrix
c = np.vstack((np.hstack((p5+p4-p2+p6,p1+p2)),
np.hstack((p3+p4,p1+p5-p3-p7))))
x = len(c) - rowDim
if (x > 0):
c = c[:-x, :] #delete padded rows
x = len(c[0]) - colDim
if (x > 0):
c = c[:,:-x] #delete padded columns
return cTimings of the Strassen Algorithm with Crossover to Numpy for Square Matrices¶
Before checking the performance on random inputs we check the performance on square matrices of size for various . The results for the first machine which is a MacBook Pro 16 with a 6-Core Intel Core i7 at 2.6 GHz with 16GB of RAM is shown in Table 2. The column headings are given shorthand names but they can be described as follows. The Numpy column contains timings in seconds for Numpy.matmul. The Strassen column contains timings in seconds for the standard Strassen algorithm shown discussed above modified from GeeksforGeeks, 2022. The Strassen16, Strassen32, etc. columns represent timings from the Python code for strassenGeneral shown above with various crossover levels. The Standard column contains timings for the standard matrix multiplication algorithm previously discussed. We see in Table 2 that using a Strassen type algorithm and crossing over to Numpy when Matrix size is 128 gives a very slight advantage over crossing over at 64. Crossing over at larger or smaller values is slower than crossing over at size 128. We also see that not crossing over at all is even slower than the standard matrix multiplication for these sizes. Since the non-crossover Strassen algorithm and the standard matrix multiplication are not competitive and very slow, we stopped timing them after the case because they would have taken a very long time to compute.
Table 3 is similar to Table 2 except we’ve removed all but the best crossover case for Strassen (crossover 128) and added columns to show the current time divided by the previous time. These latter columns are instructive because for Strassen we expect that if we double the size of the matrices the timing should increase seven-fold and it does. Similarly for the standard algorithm when we double the input size we expect the timing to increase eight-fold which it does. We don’t exactly know what to expect for Numpy without closely examining the code, but we see that for the largest 2 cases when we double the size of the inputs the timing increases 12 to 15-fold. This suggests that if we further increase the size of the matrices that the Strassen type algorithm with a crossover at size 128 will continue to be much faster than the Numpy computation for square matrices with integer entries.
Normally, we would expect a matrix multiplication to increase no more than eight-fold when we double the inputs. This suggests that Numpy is tuned for matrices of size or smaller. Alternatively, perhaps at larger sizes there are more cache misses in the Numpy algorithm. Without a close examination of the Numpy code it is not clear which is the case, but the point is that a divide and conquer algorithm such as Strassen combined with Numpy will perform better than Numpy alone on large matrices with integer entries.
Timings from a second machine are shown in Table 4. These timings are for the same experiment as above on a Windows 11 Machine with 3.0 GHz Core i7-9700 with 8 cores and 32 GB of RAM. In this case we see again that using a Strassen type algorithm that crosses over to Numpy at size 128 is considerably faster than using Numpy alone for large matrices with integer entries. Moreover we see that for the largest cases if we double the matrix size, the timings for the Strassen based algorithm will continue to grow seven-fold while the Numpy timings will grow ten-fold for each doubling of input-size.
Since both of these trials were based on Intel i7 chips, we ran a third experiment on a Linux machine with an Intel Xeon E5-2680 v3 @ 2.50GHz with 16 GB of RAM. Timings from this machine are in Table 5 and are similar to the previous tables.
Timings of the Strassen Algorithm with Crossover to Numpy for Arbitrary Matrices¶
Although the Python function strassenGeneral shown above will work for Arbitrary sized matrices, to this point we have only shown timings for square matrices where is a power of 2. The reason for this is that growth rates in timings when increases are easier to track for powers of 2. However, to show that the Strassen type algorithm with crossover is viable in general we need to test for a variety of arbitrary sizes. For this experiment it is not possible to show the results in simple tables such as Table 2 through Table 5.
To motivate the next experiment consider the sample output shown below:
(1701 x 1267) * (1267 x 1678)
numpy (seconds) 15.43970187567
numpyDot (seconds) 15.08170314133
a @ b (seconds) 15.41474305465
strassen64 (seconds) 3.980883831158
strassen128 (seconds) 2.968686999753
strassen256 (seconds) 2.88325377367
DC64 (seconds) 6.42917919531
DC128 (seconds) 4.37878428772
DC256 (seconds) 4.12086373381
(1659 x 1949) * (1949 x 1093)
numpy (seconds) 33.79341135732
numpyDot (seconds) 33.8062295187
a @ b (seconds) 33.6903500761
strassen64 (seconds) 2.929703416
strassen128 (seconds) 2.54137444496
strassen256 (seconds) 2.75581365264
DC64 (seconds) 4.581859096884
DC128 (seconds) 4.08950223028
DC256 (seconds) 4.01872271299
(1386 x 1278) * (1278 x 1282)
numpy (seconds) 7.96956253983
numpyDot (seconds) 7.54114297591
a @ b (seconds) 8.81335245259
strassen64 (seconds) 2.425855960696
strassen128 (seconds) 1.823907148092
strassen256 (seconds) 1.74107060767
DC64 (seconds) 3.8810345549
DC128 (seconds) 2.672704061493
DC256 (seconds) 2.603429134935This snippet of output shows three different matrix multiplies using three different variations of three different methods on the Linux machine with the Xeon processor mentioned above. To illustrate what this output means consider the first block of output which represents a matrix multiplied by a matrix. The first three timings are variations of Numpy. The first is Numpy.matmul, the second is Numpy.dot and the third is called via the @ operator Python.org, 2022 which is really just an infix operator that should be the same as Numpy.matmul. The next three timings are for the Strassen type algorithm with crossover to Numpy at size 64, 128, and 256. The third set of timings are Divide and Conquer matrix multiplications that crossover to Numpy at size 64, 128, and 256. These latter three methods were added since much of the increase in efficiency of the Strassen type algorithms is due to their divide and conquer approach which allows us to compute Numpy multiplications on smaller matrices. We don’t show the source code for this approach because it is not faster than the Strassen approach, however it can be produced with a simple modification of the code in strassenGeneral. The Strassen algorithm divides the first matrix into sub-matrices and the second matrix into and reassembles via seven clever products. The regular divide and conquer approach creates the final product as the four submatrices , , , and . This uses eight products but is more straightforward than Strassen and allows for recursively calling itself until crossing over to Numpy for the smaller products.
We note for the three arbitrary size matrix multiplies shown above that the Strassen based approaches are fastest, and the alternative divide and conquer approaches are two to three times faster than the Numpy method but slower than the Strassen method.
To create a good experiment we set three variables , , to random integers between 1000 and 8000 and then created two matrices one of size and the other of size . Both were filled with random integers and multiplied using the 9 methods described above. We then put this experiment into a loop to repeat several thousand times. In actuality we stopped the experiment on the MacBook and the Windows machine after about 2 weeks and we stopped the Linux machine after a few hours because the latter machine is a shared machine used by students at Rowan and the timings are not accurate when it has many users.
The question is how do we present the results of several hundred such experiments on random sized matrices in a compact manner? Since we have a large number of different dimension multiplies they cannot easily be put into a table so instead we decided to organize the results by elapsed time. To see how consider Figure 2. We bin the Strassen128 results into round number of seconds and we see the -axis of Figure 2 shows the number of seconds of Strassen128. Let us consider the case of 102 seconds. The matrix multiply took 101.56 seconds using Strassen128 and took 2482.76 seconds using Numpy. Meanwhile the matrix multiply using Strassen128 took 101.80 seconds compared to 2792.11 seconds using Numpy. These are the only 2 cases that round to 102 seconds for Strassen128 so they get bucketed together and averaged. The Average Strassen128 time for these 2 cases is 101.68 seconds and the average Numpy time for these 2 cases is 2637.43 seconds. In the Figure we normalize by Strassen128 so the Strassen128 value for 102 seconds is 1.0 and the Numpy value for 102 seconds is . Thus for matrix multiplies that take 102 seconds for Strassen128 the Numpy routines take almost 26 times as long which in this case is 44 minutes versus less than 2 for the Strassen128 routine.
Now that we’ve described how Figure 2 is derived it is useful to describe several things shown by the Figure. First note that for large matrix multiplies that take at least 15 seconds for the Strassen type algorithm that crosses over at size 128, the regular Numpy algorithms all take at least 8 times as long and in some cases up to 30 times as long. Moreover the general trend is increasing so that if we tested even larger sizes we would expect the disparity to continue to increase. Another item to notice is there is really no difference between Numpy.matmul, Numpy.dot or the infix operator a@b as expected. Also notice that the Strassen algorithms with crossover are almost twice as fast as the more straightforward divide and conquer algorithm discussed above. The last item to notice is the crossing over at size 128 seems to work best, just as in the square cases of Table 2.
Figure 3 is similar to Figure 2 except these timings are done on the Windows 11 machine described above. Here we see that the Numpy algorithms take between 8 and 16 times as long as the Strassen type algorithm that crosses over to Numpy at size 128. One other difference between the Mac and Windows machine is that crossing over at size 64 is better than crossing over at size 128 more frequently on the Windows machine.
Since the run-time to compute these last 2 figures is more than several weeks, we did not repeat the experiment on the shared machine with the Xeon processor, however we did run it for several hours and the Strassen128 algorithm seems to be 8 to 16 times faster than Numpy for cases longer than 15 seconds just as with the Mac and Windows machines.
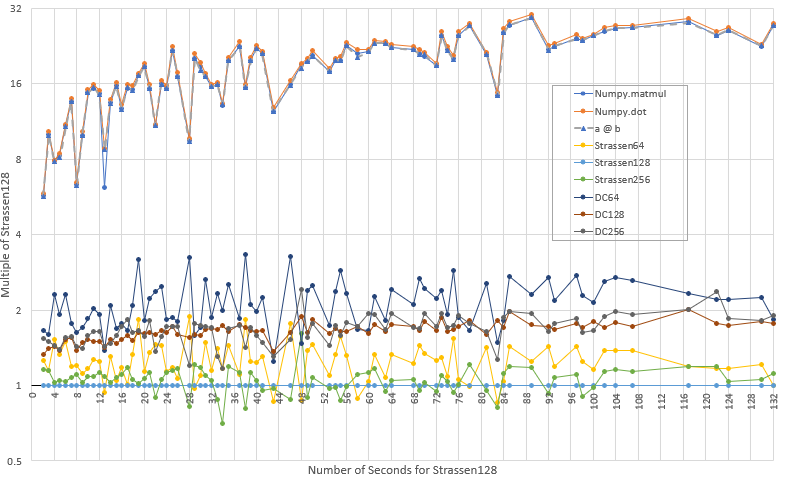
Figure 2:Timing of Multiple Algorithms Relative to Strassen128 on MacBook Pro 16 with Core i7 @ 2.6 GHz.
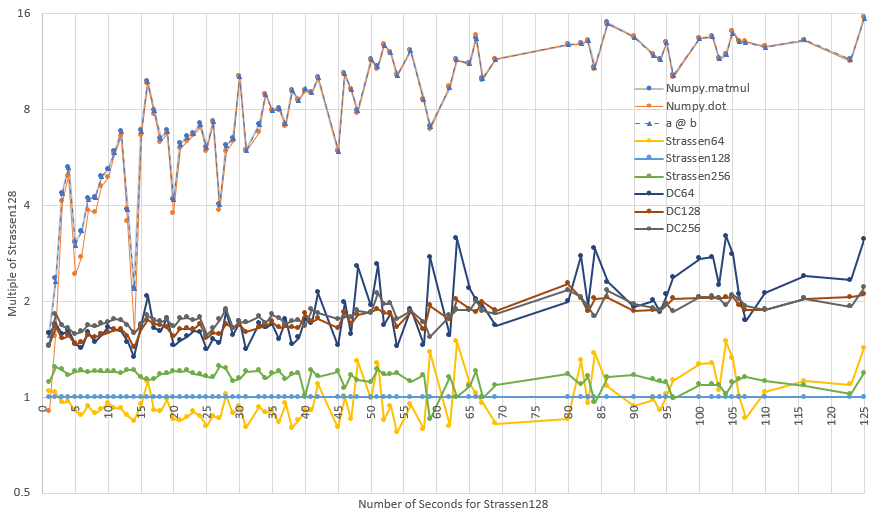
Figure 3:Timing of Multiple Algorithms Relative to Strassen128 on Windows 11 with Core i7 @ 3.0 GHz.
Conclusions¶
Numpy is a Python library which is widely used in the math and scientific community because of its speed. In this paper we presented a Strassen type algorithm that greatly improves on Numpy performance for large matrices with integer entries. For integer matrices with row dimension or column dimension in the thousands the algorithm can be 8 to 30 times faster than Numpy. The algorithm is the standard Strassen divide and conquer algorithm but it crosses over to Numpy when either the row or column dimension of one of the matrices drops below 128. The algorithm was tested on a MacBook, an I7 based Windows machine as well as a Linux machine running a Xeon processor with similar results. Although there is no apparent advantage for matrices with real entries, there are a number of applications for matrices with integer coefficients.
Copyright © 2023 Breitzman. This is an open-access article distributed under the terms of the Creative Commons Attribution 3.0 Unported license.
- Fink, Z., Liu, S., Choi, J., Diener, M., & Kale, L. V. (2021). Performance Evaluation of Python Parallel Programming Models: Charm4Py and mpi4py. 2021 IEEE/ACM 6th International Workshop on Extreme Scale Programming Models and Middleware (ESPM2), 38–44. 10.1109/ESPM254806.2021.00010
- Strassen, V. (1969). Gaussian elimination is not optimal. Numerische Mathematik, 354–356. 10.1007/BF02165411
- Harvey, D., & der Hoeven, J. V. (2018). On the complexity of integer matrix multiplication. Journal of Symbolic Computation, 1–8. 10.1016/j.jsc.2017.11.001
- Python.org. (Last Accessed December 27, 2022). PEP 465: A dedicated infix operator for matrix multiplication. Available at https://peps.python.org/pep-0465/.
- GeeksforGeeks. (Last Accessed November 23, 2022). Strassen’s Matrix Multiplication - GeeksforGeeks. Available at https://www.geeksforgeeks.org/strassens-matrix-multiplication/.
- Cormen, T. H., Leiserson, C. E., Rivest, R., & Stein, C. (2009). Introduction to Algorithms. MIT Press.
