multinterp
A Unified Interface for Multivariate Interpolation in the Scientific Python Ecosystem
Contents
from __future__ import annotations
import matplotlib.pyplot as plt
import numpy as np
from multinterp.rectilinear._multi import MultivaluedInterpConsider the following multivalued function:
def squared_coords(x, y):
return x**2 + y**2
def trig_func(x, y):
return y * np.sin(x) + x * np.cos(y)
def multivalued_func(x, y):
return np.array([squared_coords(x, y), trig_func(x, y)])As before, we can generate values on a sample input grid, and create a grid of query points.
x_grid = np.geomspace(1, 11, 1000) - 1
y_grid = np.geomspace(1, 11, 1000) - 1
x_mat, y_mat = np.meshgrid(x_grid, y_grid, indexing="ij")
z_mat = multivalued_func(x_mat, y_mat)
x_new, y_new = np.meshgrid(
np.linspace(0, 10, 1000),
np.linspace(0, 10, 1000),
indexing="ij",
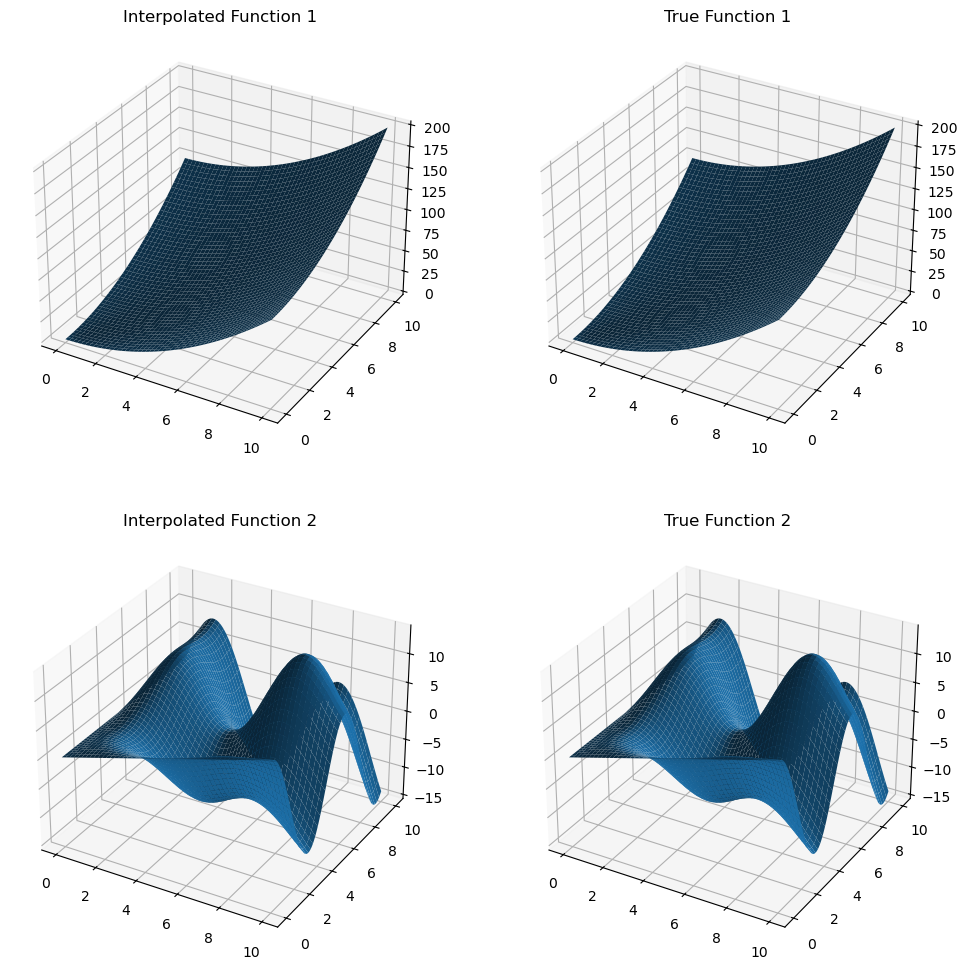
)MultivaluedInterp can easily interpolate the function at the query points and avoid repeated calculations.
mult_interp = MultivaluedInterp(z_mat, [x_grid, y_grid], backend="cupy")
z_mult_interp = mult_interp(x_new, y_new).get()
z_true = multivalued_func(x_new, y_new)
# Create a figure
fig = plt.figure(figsize=(12, 12))
# Plot the first interpolated function
ax1 = fig.add_subplot(2, 2, 1, projection="3d")
ax1.plot_surface(x_new, y_new, z_mult_interp[0])
ax1.set_title("Interpolated Function 1")
# Plot the first true function
ax2 = fig.add_subplot(2, 2, 2, projection="3d")
ax2.plot_surface(x_new, y_new, z_true[0])
ax2.set_title("True Function 1")
# Plot the second interpolated function
ax3 = fig.add_subplot(2, 2, 3, projection="3d")
ax3.plot_surface(x_new, y_new, z_mult_interp[1])
ax3.set_title("Interpolated Function 2")
# Plot the second true function
ax4 = fig.add_subplot(2, 2, 4, projection="3d")
ax4.plot_surface(x_new, y_new, z_true[1])
ax4.set_title("True Function 2")
# Display the plot
plt.show()
