
popmon: Analysis Package for Dataset Shift Detection
Abstract¶
popmon is an open-source Python package
to check the stability of a tabular dataset.
popmon creates histograms of features binned in time-slices, and compares the stability of its profiles and distributions
using statistical tests, both over time and with respect to a reference dataset.
It works with numerical, ordinal and categorical features, on both pandas and Spark dataframes,
and the histograms can be higher-dimensional, e.g. it can also track correlations between sets of features.
popmon can automatically detect and alert on changes observed over time, such as trends, shifts, peaks, outliers, anomalies, changing correlations, etc.,
using monitoring business rules that are either static or dynamic.
popmon results are presented in a self-contained report.
Introduction¶
Tracking model performance is crucial to guarantee that a model behaves as designed and trained initially, and for determining whether to promote a model with the same initial design but trained on different data to production. Model performance depends directly on the data used for training and the data predicted on. Changes in the latter (e.g. certain word frequency, user demographics, etc.) can affect the performance and make predictions unreliable.
Given that input data often change over time, it is important to track changes in both input distributions and delivered predictions periodically, and to act on them when they are significantly different from past instances – e.g. to diagnose and retrain an incorrect model in production. Predictions may be far ahead in time, so the performance can only be verified later, for example in one year. Taking action at that point might already be too late.
To make monitoring both more consistent and semi-automatic, ING Bank has
created a generic Python package called popmon. popmon monitors
the stability of data populations over time and detects dataset shifts,
based on techniques from statistical process control and the dataset
shift literature.
popmon employs so-called dynamic monitoring rules to flag and alert
on changes observed over time. Using a specified reference dataset, from
which observed levels of variation are extracted automatically,
popmon sets allowed boundaries on the input data. If the reference
dataset changes over time, the effective ranges on the input data can
change accordingly. Dynamic monitoring rules make it easy to detect
which (combinations of) features are most affected by changing
distributions.

Figure 1:The popmon package logo
popmon is light-weight. For example, only one line is required to
generate a stability report.
report = popmon.df_stability_report(
df,
time_axis="date",
time_width="1w",
time_offset="2022-1-1"
)
report.to_file("report.html")The package is built on top of Python’s scientific computing ecosystem
(numpy Harris et al., 2020, scipy Virtanen et al., 2020) and
supports pandas and Apache Spark dataframes
The pandas development team, 2020McKinney, 2010Zaharia et al., 2016.
This paper discusses how popmon monitors for dataset changes. The
popmon code is modular in design and user configurable. The project
is available as open-source software.[1]
Related work¶
Many algorithms detecting dataset shift exist that follow a similar
structure Lu et al., 2018, using various data
structures and algorithms at each step Dasu et al., 2006Qahtan et al., 2015.
However, few are readily available to use in production. popmon offers both a
framework that generalizes pipelines needed to implement those
algorithms, and default data drift pipelines, built on histograms with
statistical comparisons and profiles (see Data representation).
Other families of tools have been developed that work on individual data points, for model explanations (e.g. SHAP Lundberg & Lee, 2017, feature attributions Sturmfels et al., 2020), rule-based data monitoring (e.g. Great Expectations Gong et al., 2022, Deequ Schelter et al., 2018) and outlier detection (e.g. Rabanser et al. (2019)Lopez-Paz & Oquab (2017)).
alibi-detect Klaise et al., 2020Van Looveren et al., 2022
is somewhat similar to popmon. This is an open-source Python library
that focuses on outlier, adversarial and drift detection. It allows for
monitoring of tabular, text, images and time series data, using both
online and offline detectors. The backend is implemented in TensorFlow
and PyTorch. Much of the reporting functionality, such as feature
distributions, are restricted to the (commercial) enterprise version
called seldon-deploy. Integrations for model deployment are
available based on Kubernetes. The infrastructure setup thus is more
complex and restrictive than for popmon, which can run on any
developer’s machine.
Contributions¶
The advantage of popmon’s dynamic monitoring rules over
conventional static ones, is that little prior knowledge is required of
the input data to set sensible limits on the desired level of stability.
This makes popmon a scalable solution over multiple datasets.
To the best of our knowledge, no other monitoring tool exists that suits our criteria to monitor models in production for dataset shift. In particular, no other, light-weight, open-source package is available that performs such extensive stability tests of a pandas or Spark dataset.
We believe the combination of wide applicability, out-of-the-box performance,
available statistical tests, and configurability makes popmon an ideal
addition to the toolbox of any data scientist or machine learning
engineer.
Figure 2:Step-by-step overview of popmon’s pipeline as described in Approach onward.
Approach¶
popmon tests the dataset stability and reports the results through a
sequence of steps (Figure 2):
- The data are represented by histograms of features, binned in time-slices (Data representation).
- The data is arranged according to the selected reference type (Comparisons).
- The stability of the profiles and distributions of those histograms are compared using statistical tests, both with respect to a reference and over time. It works with numerical, ordinal, categorical features, and the histograms can be higher-dimensional, e.g. it can also track correlations between any two features (Comparisons).
popmoncan automatically flag and alert on changes observed over time, such as trends, anomalies, changing correlations, etc, using monitoring rules (Alerting).- Results are reported to the user via a dedicated, self-contained report (Reporting).
Dataset shift¶
In the context of supervised learning, one can distinguish dataset shift as a shift in various distributions:
- Covariate shift: shift in the independent variables ().
- Prior probability shift: shift in the target variable (the class, ).
- Concept shift: shift in the relationship between the independent and target variables (i.e. ).
Note that there is a lot of variation in terminology used, referring to probabilities prevents this ambiguity. For more information on dataset shift see Quiñonero-Candela et al. (2008).
popmon is primarily interested in monitoring the distributions of
features and labels for monitoring trained classifiers.
These data in deployment ideally resembles the training data. However, the package
can be used more widely, for instance by monitoring interactions between
features and the label, or the distribution of model predictions.
Temporal representation¶
popmon requires features to be distributed as a function of time
(bins), which can be provided in two ways:
- Time axis. Two-dimensional (or higher) distributions are provided, where the first dimension is time and the second is the feature to monitor. To get time slices, the time column needs to be specified, e.g. “date”, including the bin width, e.g. one week (“1w”), and the offset, which is the lower edge of one time-bin, e.g. a certain start date (“2022-1-1”).
- Ordered data batches. A set of distributions of features is provided, corresponding to a new batch of data. This batch is considered a new time-slice, and is stitched to an existing set of batches, in order of incoming batches, where each batch is assigned a unique, increasing index. Together the indices form an artificial, binned time-axis.
Data representation¶
popmon uses histogram-based monitoring to track potential dataset
shift and outliers over time, as detailed in the next subsection.
In the literature, alternative data representations are also employed,
such as kdq-trees Dasu et al., 2006. Different
data representations are in principle compatible with the popmon
pipeline, as it is similarly structured to alternative methods
(see Lu et al. (2018), c.f. Fig 5).
Dimensionality reduction techniques may be used to transform the input
dataset into a space where the distance between instances are more
meaningful for comparison, before using popmon, or in-between steps.
For example a linear projection may be used as a preprocessing step, by
taking the principal components of PCA as in
Qahtan et al. (2015). Machine learning classifiers or
autoencoders have also been used for this
purpose Lipton et al., 2018Rabanser et al., 2019 and
can be particularly helpful for high-dimensional data such as images or
text.
Histogram-based monitoring¶
There are multiple reasons behind the histogram-based monitoring
approach taken in popmon.
Histograms are small in size, and thus are efficiently stored and transferred, regardless of the input dataset size. Once data records have been aggregated feature-wise, with a minimum number of entries per bin, they are typically no longer privacy sensitive (e.g. knowing the number of records with age 30-35 in a dataset).
popmon is primarily looking for changes in data distributions.
Solely monitoring the (main) profiles of a distribution, such as the
mean, standard deviation and min and max values, does not necessarily
capture the changes in a feature’s distribution. Well-known examples of
this are Anscome’s Quartet Anscome, 1973 and the
dinosaurs datasets Matejka & Fitzmaurice, 2017, where – between
different datasets – the means and correlation between two features are
identical, but the distributions are different. Histograms of the
corresponding features (or feature pairs), however, do capture the
corresponding changes.
Implementation¶
For the creation of histograms from data records the open-source
histogrammar package has been adopted. histogrammar has been
implemented in both Scala and Python
Pivarski & Svyatkovskiy, 2021Pivarski et al., 2016,
and works on Spark and pandas dataframes respectively. The two
implementations have been tested extensively to guarantee compatibility.
The histograms coming out of histogrammar form the basis of the
monitoring code in popmon, which otherwise does not require input
dataframes. In other words, the monitoring code itself has no Spark or
pandas data dependencies, keeping the code base relatively simple.
Histogram types¶
Three types of histograms are typically used:
- Normal histograms, meant for numerical features with known, fixed ranges. The bin specifications are the lowest and highest expected values and the number of (equidistant) bins.
- Categorical histograms, for categorical and ordinal features, typically boolean or string-based. A categorical histogram accepts any value: when not yet encountered, it creates a new bin. No bin specifications are required.
- Sparse histograms are open-ended histograms, for numerical features with no known range. The bin specifications only need the bin-width, and optionally the origin (the lower edge of bin zero, with a default value of zero). Sparse histograms accept any value. When the value is not yet encountered, a new bin gets created.
For normal and sparse histograms reasonable bin specifications can be derived automatically. Both categorical and sparse histograms are dictionaries with histogram properties. New (index, bin) pairs get created whenever needed. Although this could result in out-of-memory problems, e.g. when histogramming billions of unique strings, in practice this is typically not an issue, as this can be easily mitigated. Features may be transformed into a representation with a lower number of distinct values, e.g. via embedding or substrings; or one selects the top- most frequently occurring values.
Open-ended histograms are ideal for monitoring dataset shift and outliers: they capture any kind of (large) data change. When there is a drift, there is no need to change the low- and high-range values. The same holds for outlier detection: if a new maximum or minimum value is found, it is still captured.
Dimensionality¶
A histogram can be multi-dimensional, and any combination of types is possible. The first dimension is always the time axis, which is always represented by a sparse histogram. The second dimension is the feature to monitor over time. When adding a third axis for another feature, the heatmap between those two features is created over time. For example, when monitoring financial transactions: the first axis could be time, the second axis client type, and the third axis transaction amount.
Usually one feature is followed over time, or at maximum two. The synthetic datasets in [](#synthetic-datasets contain examples of higher-dimensional histograms for known interactions.
Additivity¶
Histograms are additive. As an example, a batch of data records arrives each week. A new batch arrives, containing timestamps that were missing in a previous batch. When histograms are made of the new batch, these can be readily summed with the histograms of the previous batches. The missing records are immediately put into the right time-slices.
It is important that the bin specifications are the same between different batches of data, otherwise their histograms cannot be summed and comparisons are impossible.
Limitations¶
There is one downside to using histograms: since the data get aggregated into bins, and profiles and statistical tests are obtained from the histograms, slightly lower resolution is achieved than on the full dataset. In practice, however, this is a non-issue; histograms work great for data monitoring. The reference type and time-axis binning configuration allow the user for selecting an effective resolution.
Comparisons¶
In popmon the monitoring of data stability is based on statistical
process control (SPC) techniques. SPC is a standard method to manage the
data quality of high-volume data processing operations, for example in a
large data warehouse English, 1999. The idea is as
follows. Most features have multiple sources of variation from
underlying processes. When these processes are stable, the variation of
a feature over time should remain within a known set of limits. The
level of variation is obtained from a reference dataset, one that is
deemed stable and trustworthy.
For each feature in the input data (except the time column), the stability is determined by taking the reference dataset – for example the data on which a classification model was trained – and contrasting each time slot in the input data.
The comparison can be done in two ways:
- Comparisons: statistically comparing each time slot to the reference data (for example using Kolmogorov-Smirnov testing, testing, or the Pearson correlation).
- Profiles: for example, tracking the mean of a distribution over time and contrasting this to the reference data. Similar analyses can be done for other summary statistics, such as the median, min, max or quantiles. This is related to the CUsUM technique Page, 1954, a well-known method in SPC.
Reference types¶
Consider to be an N-dimensional dataset representing our reference data, and to be our incoming data. A covariate shift occurs when is detected. Different choices for and may detect different types of drift (e.g. sudden, gradual, incremental). is referred to as the reference dataset.
Many change-detection algorithms use a window-based solution that compares a static reference to a test window Dasu et al., 2006, or a sliding window for both, where the reference is dynamically updated Qahtan et al., 2015. A static reference is a wise choice for monitoring of a trained classifier: the performance of such a classifier depends on the similarity of the test data to the training data. Moreover, it may pick up an incremental departure (trend) from the initial distribution, that will not be significant in comparison to the adjacent time-slots. A sliding reference, on the other hand, is updated with more recent data, that incorporates this trend. Consider the case where the data contain a price field that is yearly indexed to the inflation, then using a static reference may alert purely on the trend.
The reference implementations are provided for common scenarios, such as working with a fixed dataset, batched dataset or with streaming data. For instance, a fixed dataset is common for exploratory data analysis and one-off monitoring, whereas batched or streaming data is more common in a production setting.
The reference may be static or dynamic. Four different reference types are possible:
- Self-reference. Using the full dataset on which the stability report is built as a reference. This method is static: each time slot is compared to all the slots in the dataset. This is the default reference setting.
- External reference. Using an external reference set, for example the training data of your classifier, to identify which time slots are deviating. This is also a static method: each time slot is compared to the full reference set.
- Rolling reference. Using a rolling window on the input dataset, allowing one to compare each time slot to a window of preceding time slots. This method is dynamic: one can set the size of the window and the shift from the current time slot. By default the 10 preceding time slots are used.
- Expanding reference. Using an expanding reference, allowing one to compare each time slot to all preceding time slots. This is also a dynamic method, with variable window size, since all available previous time slots are used. For example, with ten available time slots the window size is 9.
Statistical comparisons¶
Users may have various reasons to prefer a two-sample test over another. The appropriate comparison depends on our confidence in the reference dataset Richardson, 2022, and certain tests may be more common in some fields. Many common tests are related Dasu et al., 2006, e.g. the function is the first-order expansion of the KL distance function.
Therefore, popmon provides an extensible framework that allows users
to provide custom two-sample tests using a simple syntax, via the
registry pattern:
@Comparisons.register(key="jsd", description="JSD")
def jensen_shannon_divergence(p, q):
m = 0.5 * (p + q)
return (
0.5 *
(kl_divergence(p, m) + kl_divergence(q, m))
)Most commonly used test statistics are implemented, such as the Population-Stability-Index and the Jensen-Shannon divergence. The implementations of the and Kolmogorov-Smirnov tests account for statistical fluctuations in both the input and reference distributions. For example, this is relevant when comparing adjacent, low-statistics time slices.
Profiles¶
Tracking the distribution of values of interest over time is achieved via profiles. These are functions of the input histogram. Metrics may be defined for all dimensions (e.g. count, correlations), or for specific dimensions as in the case of 1D numerical histograms (e.g. quantiles). Extending the existing set of profiles is possible via a syntax similar as above:
@Profiles.register(
key=["q5", "q50", "q95"],
description=[
"5% percentile",
"50% percentile (median)",
"95% percentile"
],
dim=1,
type="num"
)
def profile_quantiles(values, counts):
return logic_goes_here(values, counts)Denote as the profile of feature at time , for example the 5% quantile of the histogram of incoming transaction amounts in a given week. Identical bin specifications are assumed between the reference and incoming data. is defined as the average of that metric on the reference data, and as the corresponding standard deviation.
The normalized residual between the incoming and reference data, also known as the “pull” or “Z-score”, is given by:
When the underlying sources of variation are stable, and assuming the reference dataset is asymptotically large and independent from the incoming data, follows a normal distribution centered around zero and with unit width, , as dictated by the central limit theorem Fischer, 2011.
In practice, the criteria for normality are hardly ever met. Typically the distribution is wider with larger tails. Yet, approximately normal behaviour is exhibited. Chebyshev’s inequality Chebyshev, 1867 guarantees that, for a wide class of distributions, no more than of the distribution’s values can be or more standard deviations away from the mean. For example, a minimum of 75% (88.9%) of values must lie within two (three) standard deviations of the mean. These boundaries reoccur in [dynamic monitoring rules].
Alerting¶
For alerting, popmon uses traffic-light-based monitoring rules,
raising green, yellow or red alerts to the user. Green alerts signal the
data are fine, yellow alerts serve as warnings of meaningful
deviations, and red alerts need critical attention. These monitoring
rules can be static or dynamic, as explained in this section.
Static monitoring rules¶
Static monitoring rules are traditional data quality rules (e.g. Rahm & Do (2000)). Denote as metric of feature at time , for example the number of NaNs encountered in feature on a given day. As an example, the following traffic lights might be set on :
The thresholds of this monitoring rule are fixed, and considered static over time. They need to be set by hand, to sensible values. This requires domain knowledge of the data and the processes that produce it. Setting these traffic light ranges is a time-costly process when covering many features and corresponding metrics.
Dynamic monitoring rules¶
Dynamic monitoring rules are complementary to static rules. The levels of variation in feature metrics are assumed to have been measured on the reference data. Per feature metric, incoming data are compared against the reference levels. When (significantly) outside of the known bounds, instability of the underlying sources is assumed, and a warning gets raised to the user.
popmon’s dynamic monitoring rules raise traffic lights to the user
whenever the normalized residual falls outside
certain, configurable ranges. By default:
If the reference dataset is changing over time, the effective ranges on can change as well. The advantage of this approach over static rules is that significant deviations in the incoming data can be flagged and alerted to the user for a large set of features and corresponding metrics, requiring little (or no) prior knowledge of the data at hand. The relevant knowledge is all extracted from the reference dataset.
With multiple feature metrics, many dynamic monitoring tests can get performed on the same dataset. This raises the multiple comparisons problem: the more inferences are made, the more likely erroneous red flags are raised. To compensate for a large number of tests being made, typically one can set wider traffic light boundaries, reducing the false positive rate.[2] The boundaries control the size of the deviations - or number of red and yellow alerts - that the user would like to be informed of.
Reporting¶
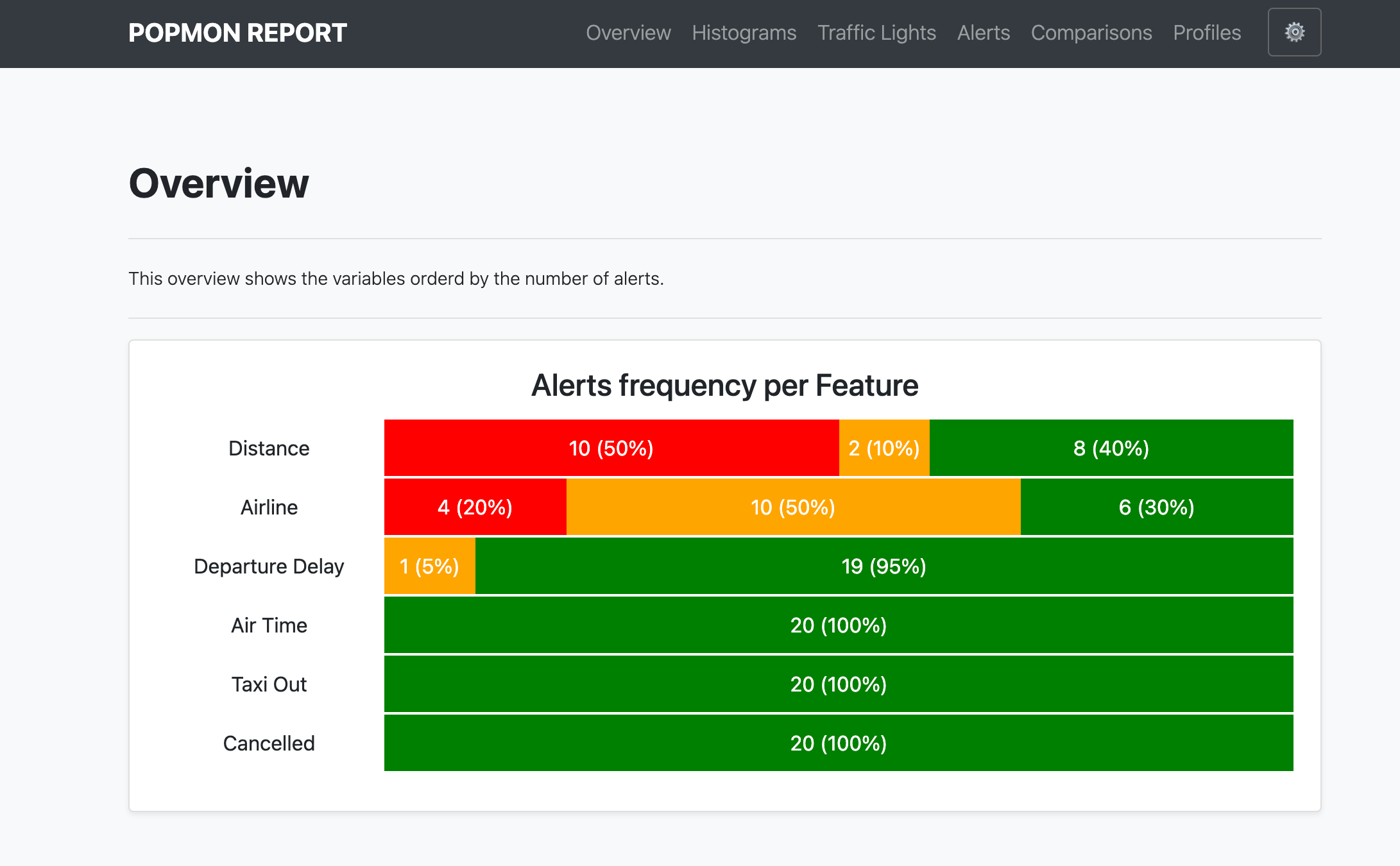
Figure 3:A snapshot of part of the HTML stability report. It shows the aggregated traffic light overview. This view can be used to prioritize features for inspection.
popmon outputs monitoring results as HTML stability reports. The
reports offer multiple views of the data (histograms and heatmaps), the
profiles and comparisons, and traffic light alerts. There are several
reasons for providing self-contained reports: they can be opened in the
browser, easily shared, stored as artifacts, and tracked using
tools such as MLFlow. The reports also have no need for an advanced
infrastructure setup, and are possible to create and view in many
environments: from a local machine, a (restricted) environment, to a public
cloud. If, however, a certain dashboarding tool is available, then the
metrics computed by popmon are exposed and can be exported into
that tool, for example Kibana Elastic, 2022. One downside of producing
self-contained reports is that they can get large when the plots are
pre-rendered and embedded. This is mitigated by embedding plots as
JSON that are (lazily) rendered on the client-side. Plotly express
Plotly Development Team, 2022 powers the interactive embedded plots in popmon
as of v1.0.0.
Note that multiple reference types can be used in the same stability
report. For instance, popmon’s default reference pipelines always
include a rolling comparison with window size 1, i.e. comparing to the
preceding time slot.
Synthetic datasets¶
In the literature synthetic datasets are commonly used to test the
effectiveness of dataset shift monitoring approaches
Lu et al., 2018. One can test the detection for
all kinds of shifts, as the generation process
controls when and how the shift happens. popmon has been tested on multiple of such
artificial datasets: Sine1, Sine2, Mixed, Stagger, Circles, LED, SEA and
Hyperplane
Pesaranghader et al., 2018Street & Kim, n.d.Fan, 2004.
These datasets cover myriad dataset shift characteristics: sudden and
gradual drifts, dependency of the label on just
one or multiple features, binary and multiclass labels, and containing
unrelated features. The dataset descriptions and sample popmon
configurations are available in the code repository.
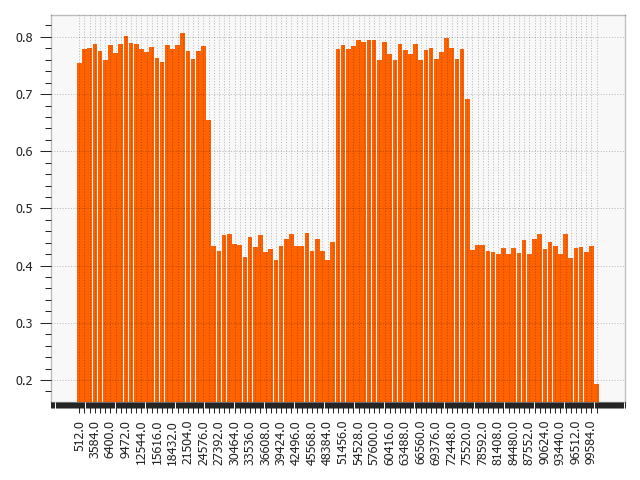
Figure 4:LED: Pearson correlation compared with previous histogram. The shifting points are correctly identified at every 5th of the LED dataset. Similar patterns are visible for other comparisons, e.g. .
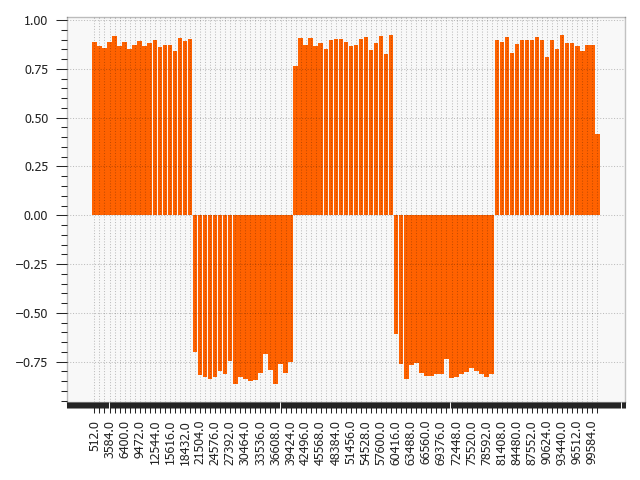
Figure 5:Sine1: The dataset shifts around data points 20.000, 40.000, 60.000 and 80.000 of the Sine1 dataset are clearly visible.
The reports generated by popmon capture features and time bins where
the dataset shift is occurring for all tested datasets. Interactions between features
and the label can be used for feature selection, in addition to monitoring the individual
feature distributions. The sudden and gradual drifts are clearly visible
using a rolling reference, see Figure 4 for examples.
The drift in the Hyperplane dataset, incremental and gradual, is not expected to be detected
using a rolling reference or self-reference. Moreover, the dataset is synthesized so that the distribution of
the features and the class balance does not change Fan, 2004.
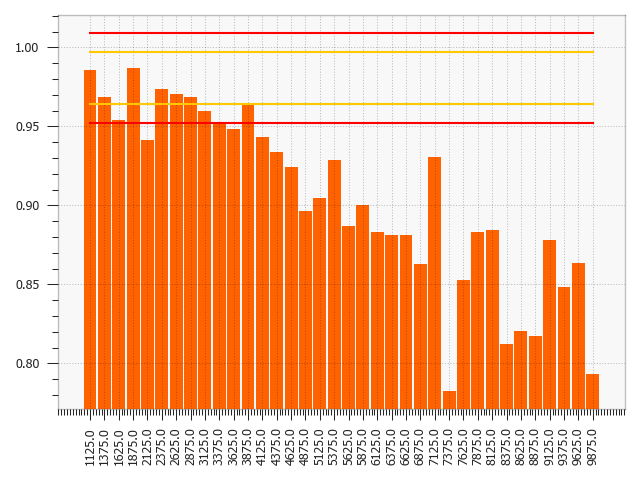
Figure 6:Hyperplane: The incremental drift compared to the reference dataset is observed for the PhiK correlation between the predictions and the label.
The process to monitor this dataset could be set up in multiple ways, one of which is described here.
A logistic regression model is trained on the first 10% of the data, which is also used as static reference.
The predictions of this model are added to the dataset, simulating a machine learning model in production.
popmon is able to pick up the divergence between the predictions and the class label, as depicted
in Figure 6.
Conclusion¶
This paper has presented popmon, an open-source Python package to
check the stability of a tabular dataset. Built around histogram-based
monitoring, it runs on a dataset of arbitrary size, supporting both pandas and
Spark dataframes. Using the variations observed in a reference dataset,
popmon can automatically detect and flag deviations in incoming
data, requiring little prior domain knowledge. As such, popmon is a
scalable solution that can be applied to many datasets. By default its
findings get presented in a single HTML report. This makes popmon
ideal for both exploratory data analysis and as a monitoring tool for
machine learning models running in production.
We believe the combination of out-of-the-box performance and presented features makes popmon an
excellent addition to the data practitioner’s toolbox.
We thank our colleagues from the ING Analytics Wholesale Banking team
for fruitful discussions, all past contributors to popmon, and in
particular Fabian Jansen and Ilan Fridman Rojas for carefully reading
the manuscript. This work is supported by ING Bank.
Copyright © 2022 Brugman et al. This is an open-access article distributed under the terms of the Creative Commons Attribution 3.0 Unported license.
See https://
github .com /ing -bank /popmon for code, documentation, tutorials and example stability reports. Alternatively one may apply the Bonferroni correction to counteract this problem Bonferroni, 1936.
- SPC
- statistical process control
- Harris, C. R., Millman, K. J., van der Walt, S. J., Gommers, R., Virtanen, P., Cournapeau, D., Wieser, E., Taylor, J., Berg, S., Smith, N. J., Kern, R., Picus, M., Hoyer, S., van Kerkwijk, M. H., Brett, M., Haldane, A., del Río, J. F., Wiebe, M., Peterson, P., … Oliphant, T. E. (2020). Array programming with NumPy. Nature, 585(7825), 357–362. 10.1038/s41586-020-2649-2
- Virtanen, P., Gommers, R., Oliphant, T. E., Haberland, M., Reddy, T., Cournapeau, D., Burovski, E., Peterson, P., Weckesser, W., Bright, J., van der Walt, S. J., Brett, M., Wilson, J., Millman, K. J., Mayorov, N., Nelson, A. R. J., Jones, E., Kern, R., Larson, E., … SciPy 1.0 Contributors. (2020). SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nature Methods, 17, 261–272. 10.1038/s41592-019-0686-2
- The pandas development team. (2020). pandas-dev/pandas: Pandas (latest) [Computer software]. Zenodo. 10.5281/zenodo.3509134
- Wes McKinney. (2010). Data Structures for Statistical Computing in Python. In Stéfan van der Walt & Jarrod Millman (Eds.), Proceedings of the 9th Python in Science Conference (pp. 56–61). 10.25080/Majora-92bf1922-00a
- Zaharia, M., Xin, R. S., Wendell, P., Das, T., Armbrust, M., Dave, A., Meng, X., Rosen, J., Venkataraman, S., Franklin, M. J., Ghodsi, A., Gonzalez, J., Shenker, S., & Stoica, I. (2016). Apache Spark: A Unified Engine for Big Data Processing. Commun. ACM, 59(11), 56–65. 10.1145/2934664
- Lu, J., Liu, A., Dong, F., Gu, F., Gama, J., & Zhang, G. (2018). Learning under concept drift: A review. IEEE Transactions on Knowledge and Data Engineering, 31(12), 2346–2363. 10.1109/TKDE.2018.2876857
- Dasu, T., Krishnan, S., Venkatasubramanian, S., & Yi, K. (2006). An information-theoretic approach to detecting changes in multi-dimensional data streams. In Proc. Symp. on the Interface of Statistics, Computing Science, and Applications.
- Qahtan, A. A., Alharbi, B., Wang, S., & Zhang, X. (2015). A pca-based change detection framework for multidimensional data streams: Change detection in multidimensional data streams. Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 935–944. 10.1145/2783258.2783359
- Lundberg, S. M., & Lee, S.-I. (2017). A unified approach to interpreting model predictions. Advances in Neural Information Processing Systems, 30.
- Sturmfels, P., Lundberg, S., & Lee, S.-I. (2020). Visualizing the Impact of Feature Attribution Baselines. Distill. 10.23915/distill.00022
- Gong, A., Campbell, J., Superconductive, & Great Expectations. (2022). Great Expectations. 10.5281/zenodo.5683574
- Schelter, S., Lange, D., Schmidt, P., Celikel, M., Biessmann, F., & Grafberger, A. (2018). Automating Large-Scale Data Quality Verification. Proc. VLDB Endow., 11(12), 1781–1794. 10.14778/3229863.3229867
- Rabanser, S., Günnemann, S., & Lipton, Z. (2019). Failing loudly: An empirical study of methods for detecting dataset shift. Advances in Neural Information Processing Systems, 32. https://proceedings.neurips.cc/paper/2019/hash/846c260d715e5b854ffad5f70a516c88-Abstract.html
- Lopez-Paz, D., & Oquab, M. (2017). Revisiting classifier two-sample tests. International Conference on Learning Representations.
- Klaise, J., Van Looveren, A., Cox, C., Vacanti, G., & Coca, A. (2020). Monitoring and explainability of models in production. arXiv Preprint arXiv:2007.06299. 10.48550/arXiv.2007.06299
