
Redist, a python tool for model-agnostics binned-likelihood fits in High Energy Physics
Abstract¶
Current High Energy Physics measurements rely on analysing the data by using underlying theoretical assumptions in model building that do not account for possible deviations from the nominal model on which the assumptions are based. This approach can introduce potential bias in parameter extraction and complicate the reinterpretation of measurements without fully reanalyzing the data. Redist is a package for building model-agnostic binned-likelihood fits, allowing combination and enhancing the reinterpretation of datasets. Redist allows direct inference of theoretical parameters of any beyond the Standard Model scenario through histogram reweighting, properly taking into account changes in kinematic distributions. By leveraging truth-level observables and capturing correlations, Redist can be interfaced with different theoretical backends to connect theoretical parameters with the pyhf environment for fitting. We present a Redist-HAMMER interface that has been developed to address direct Beyond the Standard Model measurements by reinterpreting existing datasets collected by various High Energy Physics collaborations, using the increasingly popular theoretical backend HAMMER. This enables model-agnostic interpretation of data—a crucial step for advancing precision flavor physics. Further applications of the Redist package in different fields, along the lines of the Redist-HAMMER interface in High Energy Physics, to extend pyhf models are possible and straightforward to implement.
1Introduction¶
As High Energy Physics (HEP) is entering a high-precision measurements era, minimizing assumptions about theoretical models in the data analysis becomes necessary for testing alternative interpretations on the same data. Usually HEP analyses rely on theoretical assumptions, such as the Standard Model (SM) predictions or the shapes of simulated samples produced based on a set underlying kinematic assumptions. These inherent dependencies make reinterpretation of datasets collected by the the LHCb Collaboration, 2008 and Belle II Brodzicka et al., 2012 collaborations, leading the field of flavour physics, challenging. To avoid necessarily generating simulated samples for each Beyond the Standard Model (BSM) scenario, tools like the HAMMER Bernlochner et al., 2020 or the EOS Dyk & others, 2022 packages have been developed, giving access to frameworks to adjust simulation-derived models to arbitrary BSM scenarios by reweighting the kinematic distributions of the particles to any assumption differing from the SM, also allowing to vary theoretical parameters of the chromodynamics of the events, known as Form Factors (FFs). Handling FFs is very important specifically in the study of beauty-meson decays involving neutrinos in the final state. The HAMMER interface, in particular, makes use of truth-level kinematic information, meaning the real momentum components and particle identity of the simulated particles, in the initial and final states to apply an event-by-event weighting. It allows to vary the Form Factor parametrization, from the one that has been used in the simulation production to the one that is desired for the analysis. The HAMMER interface also allows testing different BSM scenarios by assigning weights to the events on the basis of the different NP contributions associated with the Effective Field Theory (EFT) Pich, 1998 operators listed in Table 1. In general for each operator two contributions to the Wilson Coefficients are defined respectively representing the real and imaginary parts of the Wilson Coefficient.
Table 1:List of the EFT operators implemented in HAMMER. The symbols and represent the up-like and the down-like quarks involved in the vertex, as the symbols and represent the lepton and the neutrino. The pedestals and represent the chiral-state of the particles (right-, or left-handed). Any operator involving right-handed neutrinos implemented in HAMMER has been excluded from this list.
| Current type | WC Name | NP operator |
|---|---|---|
| Standard Model | ||
| Vector | ||
| Scalar | ||
| Tensor |
Python is becoming increasingly popular in High Energy Physics (HEP) analysis due to its flexibility, ease of use and the growing number of scientific tool implemented on it. At the same time, the HAMMER package is gaining traction in the community as a powerful framework to reinterpret previously analyzed datasets and explore BSM scenarios through FFs reweighting. The Redist-HAMMER (github repository) is the first full Pythonic interface between the HAMMER package and a fitting environment, by integrating it with the pyhf framework Heinrich et al., n.d. Heinrich et al., 2021. This allows HAMMER-processed samples to be used directly within pyhf’s binned-likelihood models Cranmer et al., 2012, via the Redist modifiers of the likelihood, encoding the BSM and FF dependence of the shapes as defined by the HAMMER theoretical backend. Other efforts, such as the RooHammerModel García Pardiñas et al., 2022, have been spent to address similar functionalities in the C++-based RooFit-HistFactory framework Verkerke & Kirkby, 2003. Redist-HAMMER builds on this idea by bringing it into the Python ecosystem, providing a flexible reinterpretation tool that supports combination and fitting workflows entirely in Python allowing for an easy to start interface to apply reinterpretation of HEP datasets.
The structure of this document is as follows: Section 2 describes the Redist environment and the custom modifier functionalities implemented as an extension of pyhf, Section 3 describes the Redist-HAMMER interface to pyhf with a specific focus on the methods to start coding with it and perform simple fits, Section 4 shows a set of proof of usage of the package discussing advantages of the methods that are used, finally Section 5 provides an outlook on further implementation of the Redist package in HEP and in multiple different fields of science.
2The pyhf and the Redist package¶
The pyhf package implements a very popular model building method for binned-likelihood fits. The most generic binned-likelihood can be written as the product of three components:
defined respectively as the data likelihood, , and two components introducing the experimental and theoretical constraints, and . is defined, according to the binned nature of the model, as the product of Poisson probabilities of the yields observed in data, , and the expected number of events, :
where each channel represents a different and disjoint binned distribution and bins correspond to the histogram bins. The rates are functions of constrained and unconstrained parameters, respectively defined as and . The constraints applied on the parameters might come from both experimental or theoretical priors, whose definition in the likelihood is contained in the and terms:
where the index represents the two types of constraints, and represents the auxiliary data enforcing the constraints.
The pyhf package requires the rates of the different contributions of the model to be defined as the expected number of events taken from simulation, allowing the definition of a set of modifiers which will change the rates in the fit on the depencence of the given degrees of freedom. Different types of modifiers are already defined in pyhf, so that the event rate for a given channel and bin is defined as:
where samples represents the set of contributions appearing in the same channel, is the initial event rate, and and are respectively multiplicative and additive modifiers. One challenge with defining the rates in terms of the modifiers is that it may be complicated to capture more intricate dependencies, particularly if the degrees of freedom and are expressed as the NP coefficients from the HAMMER package or as FF parameters.
The Redist package Gärtner et al., 2024 addresses this problem with a reinterpretation method where the binned event counts are updated on the basis of the new kinematic assumptions. The method has been implemented in the pyhf fitting interface through the definition of a custom modifier of the likelihood: a modifier varying event rates, computed by custom functions or external theoretical backends. The Pythonic interface of the HAMMER package has been used to build an interface between HAMMER and a generic Python-based fitting interface, while the Redist package has been implemented with a new custom modifier to use the HAMMER-weighted histograms in the definition of the pyhf models.
This implementation of Redist-HAMMER allows us to make use of the HAMMER package directly in our fits and is a valuable example of how the Redist weighting method can be applied easily to specific cases by interfacing HEP theory packages to the pyhf fitting environment.
3The Redist-HAMMER interface¶
The Redist-HAMMER follows a deliberately nested class structure, where each class is responsible for a narrowly defined task, adhering to the principle of single responsibility. Higher-level classes delegate specific subtasks to lower-level components, which are composed as objects within them. This design, while seemingly convoluted, promotes clarity, testability and separation of concerns by ensuring that each layer handles only its designated function and relies on contained objects for more granular operations. This modular, layered structure enables to effectively apply both unit and integration testing to validate each class’s behavior both in isolation and in collaboration with the other components. The structure of the package and its purpose, with respect to the HAMMER interface and pyhf, are summarized in Figure 1.
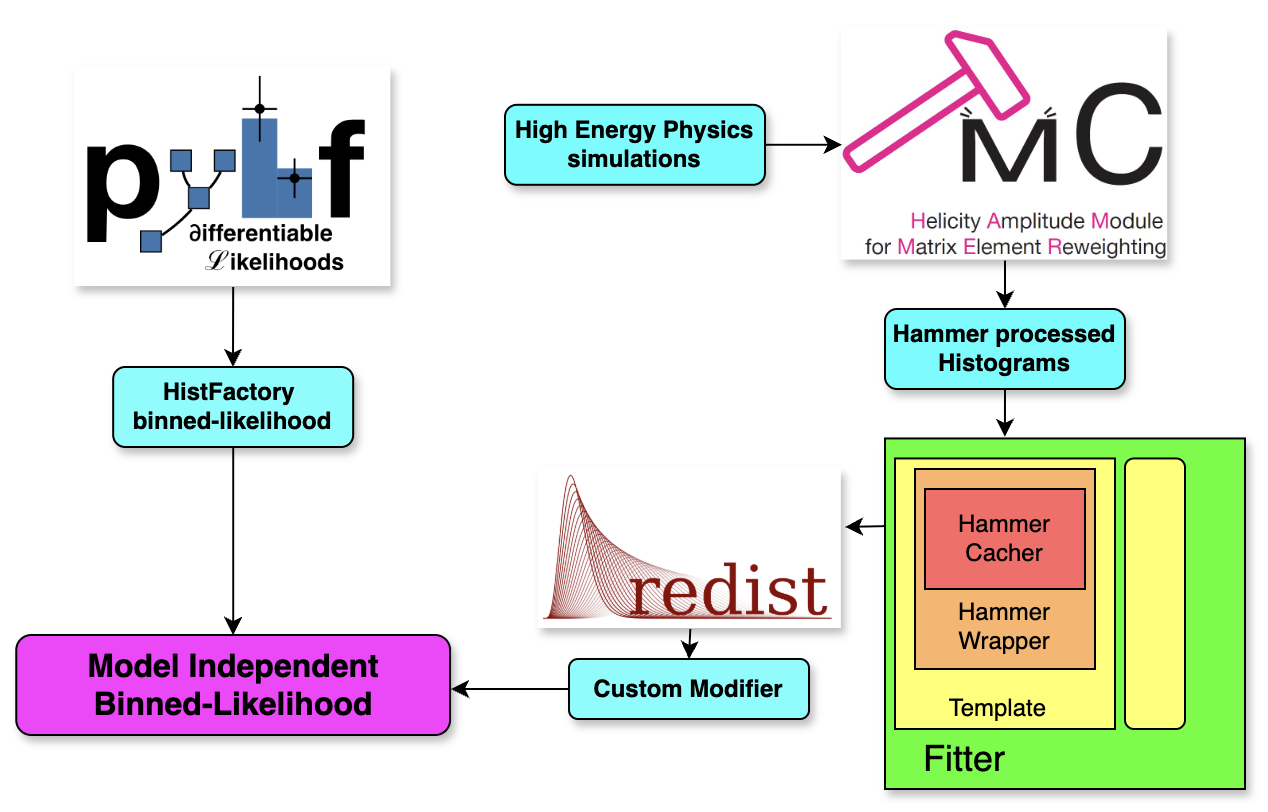
Figure 1:System diagram of the Redist package allowing HAMMER processed samples to be used in pyhf inference. The nested structure of the Redist-HAMMER interface is summarized.
The most inner object in the nested structure is the HammerCacher, a class that uses the Python HAMMER interface functions to read from a file a HAMMER-processed histograms, which are created applying HAMMER to the simulations and contain the HAMMER weighting parameters (generally ~10-20 new degrees of freedom for describing the FF parametrization and BSM injection) and the mathematical tools to extrapolate the variations of the shape as function of them. The HammerCacher stores the bin content of the HAMMER-processed histogram and updates it on the basis of any set of NP and FF parameters that were defined at HAMMER processing time. To avoid useless iterations with the HAMMER weighting, a caching procedure for the values of the parameters has been used: the values of the NP and FF parameters are stored, and the histogram bin content is updated only when the parameters are effectively varied. Multiple HammerCacher instances can be embedded in the same object and their parameters varied at the same time using the MultiHammerCacher. In addition the HammerNuisWrapper is defined as the one that contains a HammerCacher and attaches a set of multiplicative parameters to vary the bin content of the HAMMER histogram. A similar structure has been built to include non-HAMMER-weighted contributions in the model, meaning regular histograms produced from HEP simulations; the shapes of these contributions are defined by reading a file, and from the set of multiplicative parameters—representing, for example, the yields. Each NuisWrapper is further contained in a Template class, which defines an object allowing access to the bin content of the contributions and enabling changes to the parameters. The Template class also contains options to generate toy samples or to return the whole template histogram for a specific injection of parameters. Multiple Templates are stored in a single Fitter object, which is used to represent what in pyhf would be defined as a Channel, and it is used to interface the preceding nested structure of classes to Redist.
An additional class named Reader is taking care of model construction using the configurations included in a single JSON file:
{
"B02DstTauNu": {
"fileNames": ["File_containing_a_histogram.dat"],
"histoname": "Name_of_the_histogram",
"ffscheme": {
"name":"SchemeBLPRXP",
"Process":"BtoD*",
"SchemeVar":"BLPRXPVar"
},
"wcscheme": "BtoCMuNu",
"scalefactor": 1.0,
"formfactors": {
"delta_RhoSq": 1.5,
"delta_cSt": 2.0
},
"wilsoncoefficients": {
"SM": [1.0,0.0],
"S_qLlL": [0.0,0.0]
},
"nuisance": {
"Luminosity": 1.
},
"ishammerweighted": true,
"injectNP":true,
"axistitles": [
"title"
],
"strides":[1],
"binning": [[0.0, 10.0]]
}
}The path to the file containing the HAMMER-processed histogram is specified, together with all the information required to read the histogram—namely, the name and the FF scheme used in the HAMMER processing. Other options are included to define the HAMMER parameters to be handled and to organize a multi-channel model, such as “injectNP” to tag some of the contributions as purely SM, or “ishammerweighted” to distinguish contributions that are not HAMMER-processed. A scalefactor is attached to the contributions to apply a fixed pre-scaling to the yield of the contributions. Finally, information useful at plotting time, such as axis titles and binnings, is included.
Given a JSON file structured as the one above, a Fitter can be easily produced simply by using the Reader object, letting the machinery compose the nested structure on top of which the Fitter sits:
import pyhf
import json
from redist import modifier
from redist import modifier_hammer
reader = modifier_hammer.Reader("config.json")
fitter = reader.createFitter(True) # True enables a Verbose creation of the Fitterthen the Fitter object allows easy handling of the HAMMER-processed contributions and their degrees of freedom—for example, generating pseudo-data where, for a given injection of NP and FF parameters, a binned distribution is produced according to a Poissonian distribution for each bin:
params_0 = {"SM" : 1.,"Re_S_qLlL" : 0.,"Im_S_qLlL" : 0. ,
"delta_RhoSq" : 0.,"delta_cSt" : 0. ,
"Luminosity": 1.}
toy_data = fitter.get_template(0).generate_toy(**params_0)
# generate_toy() produces according to a Poisson distribution
# generate_template() to produce the exact value without fluctuations
fitter.upload_data(toy_data) # store a toy_data to be accessed as fitter._dataGiven these very simple ingredients, it is now straightforward to operatively apply the Redist method by defining the custom modifier_hammer class, inheriting from the original modifier, interfacing it with the Fitter. The original modifier class can be easily adapted in the same way to any other interface.
4Using HAMMER in pyhf¶
Finally it is possible to operatively apply the Redist weighting method in pyhf. A static reference distribution needs to be defined, together with an alternative distribution that is a function of the parameters of interest:
SM_distribution = fitter.get_template(0).generate_toy(**params_0)
def SM_B02DstTauNu():
return SM_distribution
def NP_B02DstTauNu(**kwargs):
params_NP = {"SM": 1.,
"Re_S_qLlL": **kwargs["Re_S_qLlL"],
"Im_S_qLlL": **kwargs["Im_S_qLlL"],
"delta_RhoSq": **kwargs["delta_RhoSq"],
"delta_cSt": **kwargs["delta_cSt"],
"Luminosity": 1.}
NP_distribution = fitter.get_template(0).generate_template(**params_NP)
return NP_distributionthese functions will effectively be used to create the custom modifier and vary the shape of the histogram by multiplying the initial distribution by the ratio of the two functions:
where is the shape of the template as a function of the parameters , is the reference hypothesis distribution, and is the alternative distribution. A set of parameters is then defined and the custom modifier created. The custom modifier is assigned a name to distinguish it from other types of standard modifiers and is added later to an already existing, but not custom, pyhf model through the expand_pdf attribute:
new_params = {
"Re_S_qLlL": {
"inits": (0.0,),
"bounds": ((-3.0, 3.0),),
"paramset_type": "unconstrained"
},
"Im_S_qLlL": {
"inits": (0.0,),
"bounds": ((-3.0, 3.0),),
"paramset_type": "unconstrained"
},
"delta_RhoSq": {
"inits": (0.0,),
"bounds": ((-3.0, 3.0),),
"paramset_type": "unconstrained"
},
"delta_cSt": {
"inits": (0.0,),
"bounds": ((-3.0, 3.0),),
"paramset_type": "unconstrained"
}
}
cmod = modifier_hammer.Modifier_Hammer(
new_params,
NP_B02DstTauNu,
SM_B02DstTauNu,
name="mod_B02DstTauNu"
)
spec = {
"channels": [
{
"name": "RDsMuonic",
"samples": [
{
"name": "B02DstTauNu",
"data": SM_distribution.tolist(),
"modifiers": [
{
"name": "mu",
"type": "normfactor",
"data": None,
}
],
},
]
}
]
}
model = pyhf.Model(spec)
custom_mod_B02DstTauNu = {
"name": "mod_B02DstTauNu_theory",
"type": "mod_B02DstTauNu",
"data": {"expr": "mod_B02DstTauNu_weight_fn"},
}
expanded_pyhf = {**cmod_B02DstTauNu.expanded_pyhf}
model = modifier.add_to_model(
model,
["RDsMuonic"],
["B02DstTauNu"],
expanded_pyhf,
custom_mod_B02DstTauNu
)The pyhf model contains and handles degrees of freedom associated with HAMMER-processed histograms for model-agnostic fits and reinterpretation. More generically, following the same prescription, the pyhf model is able to handle arbitrarily complex degrees of freedom where the effect of changing the templates is completely determined by the initial and alternative hypothesis we define as simple python functions.
This method has direct application in HEP analysis, in particular for the reinterpretation of semileptonic analyses. Taking, for example, the semileptonic modes of the beauty mesons and , notably, tension exists between the expected ratio of the abundance of the two decay modes and the measured ratio of the respective Branching Fractions (BF):
has been observed Banerjee et al., 2024. The Redist method, implemented with the theoretical HAMMER backend, allows to disentangle the tension and study the BSM processes in these decays in an innovative and model-independent way. The HAMMER-weighted sample can be accessed, and a template fit can be applied to study the sensitivity on the parameters of interest given a certain statistical power, defined by the number of events of the template dataset used in the fit. The phase space of the real and imaginary parts of the Wilson Coefficient associated with a scalar-like NP contribution, coupling particles and antiparticles in the same chiral state, has been inspected using a template generated with the RapidSim tool Cowan et al., 2017 and containing events. The fit has been done using a pseudo-dataset identical to the template itself, with different injections of NP, to demonstrate the application of the Redist-HAMMER interface in a small and simple sensitivity study context. This represents a simple and practical example of a use case in flavour physics data analysis, demonstrating the functionalities of maximum-likelihood-fits, generation of pseudodatasets and phase space scanning for confidence level determination.
A Negative-Logarithmic-Likelihood (NLL) fit is performed to find the optimal point, then further fits are applied over a grid of points in the phase space of the real and imaginary parts of the NP Wilson Coefficients. For each point, the NP Wilson Coefficients are fixed, while the rest of the parameters, for instance the SM contributions, are free to float to maximize the NLL. If the grid of phase space is defined with sufficiently fine granularity, this method allows inferring 2-Dimensional (2D) Confidence Intervals (CI) correctly, taking into account correlations among the parameters as shown in Figure 2.
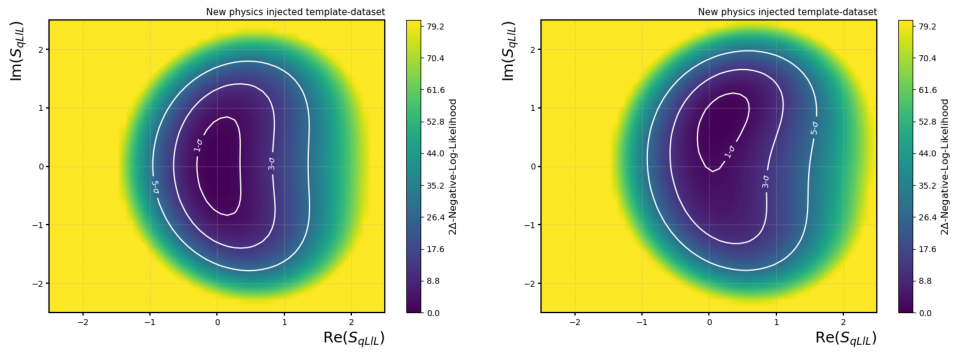
Figure 2:Negative-Log-Likelihood phase-space scan of the scalar Wilson Coefficient on a template-dataset with no NP injection (left) and on a template dataset with the NP injection of and (right). The confidence levels correspontent to 1, 3 and 5 standard deviations are overlaid to both the scans. Both the fits correctly identify the injected New Physics values showing the effectiveness of the method.
In fact, the custom modifiers applying the weighting can be mixed with the already existing shape modifiers in pyhf. This is particularly important as, generically speaking, multiple templates will compose a single channel, and some of them might not be derived from HAMMER-processed histograms, and might require other parameters for the fit. Shape modifiers like the standard histosys of pyhf can also be assigned to the HAMMER-weighted derived templates, for example to represent the variation of a different parameter, or to embed the impact of one of the HAMMER parameters that is not explicitly set free to float in the fit by defining the model as:
spec = {
"channels": [
{
"name": "RDsMuonic",
"samples": [
{
"name": "B02DstTauNu",
"data": SM_distribution.tolist(),
"modifiers": [
{
"name": "mu",
"type": "normfactor",
"data": None,
},
{
"name": "my_histosys",
"type": "histosys",
"data": {"hi_data": hi_temp.tolist(), "lo_data": lo_temp.tolist()},
}
],
},
]
}
]
}where the hi_temp and lo_temp are obtained from the shapes of the contributions with different FFs or WCs injected. An example of this usage, where the two alternative shapes hi_temp and lo_temp have been defined with respect to different injections of a FF parameter (), is shown in Figure 3.
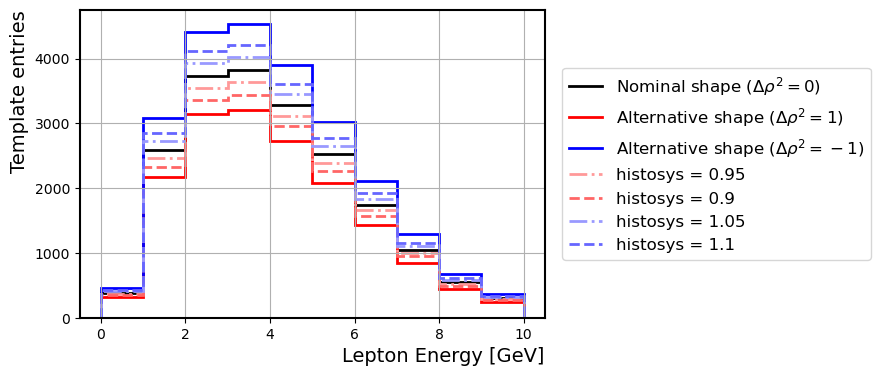
Figure 3:Distributions of a 1-dimensional pyhf template for different values of the histsys modifier, defined with respect to two different injection of values of the FF parameter in HAMMER. Redist-HAMMER allows the integration of the theoretical uncertainty on the Form Factor parameter as a standard histosys nuisance parameter in pyhf.
5Outlook¶
We present the Redist-HAMMER interface, an extension of the already existing Redist module to interface HAMMER with the fitting environment of pyhf. The package has been developed to address the challenge of direct NP measurements through the reinterpretation of the LHCb and Belle datasets, which will be a crucial step for getting a further and deeper understanding of tensions of HEP measurements with SM predictions. The module offers the possibility of easily handling very complex parameters, such as the Wilson Coefficients and the Form Factors, using the HAMMER package as theoretical backend.
Allowing for a correct reinterpretation of data also opens the possibility of combining different datasets in a single coherent fitting environment. The Redist-HAMMER interface has been validated, and studies on the benefits of a coherent combination in a simultaneous fit of different datasets, representing different decay modes, are currently ongoing. By combining different datasets in a simultaneous fit, the degrees of freedom that are shared lead to an enhancement of the sensitivity and possibly to the cancellation of biases that might arise in a post-fit average of different results.
Redist-HAMMER offers a simple and fully pythonic approach to otherwise very complex problems and has already been used to validate other studies on the Wilson Coefficients, such as the recent, and currently in development, simulation-based interface of ROOT.
What has been shown in this document represents one of the many applications, in HEP and beyond, of the Redist weighting method for model building. Future efforts will integrate other popular theoretical backends in flavour physics like Flavio Straub, 2018, finally allowing data analysts effortless use of, and possibly toggling between, all the different packages.
Fields outside HEP can benefit from the Redist method for building model-independent fits, enabling interpretation of observed patterns in complex systems without relying on predefined models.
Copyright © 2025 Colonna et al. This is an open-access article distributed under the terms of the Creative Commons Attribution 4.0 International license, which enables reusers to distribute, remix, adapt, and build upon the material in any medium or format, so long as attribution is given to the creators.
- BSM
- Beyond the Standard Model
- EFT
- Effective Field Theory
- FF
- Form Factor
- HEP
- High Energy Physics
- SM
- Standard Model
- Collaboration, Lhc. (2008). The LHCb Detector at the LHC. JINST, 3, S08005. 10.1088/1748-0221/3/08/S08005
- Brodzicka, J., Browder, T., Chang, P., Eidelman, S., Golob, B., Hayasaka, K., Hayashii, H., Iijima, T., Inami, K., Kinoshita, K., Kwon, Y., Miyabayashi, K., Mohanty, G., Nakao, M., Nakazawa, H., Olsen, S., Sakai, Y., Schwanda, C., Schwartz, A., … for the Belle Collaboration. (2012). Physics achievements from the Belle experiment. In Progress of Theoretical and Experimental Physics (Vol. 2012, p. 04D001). 10.1093/ptep/pts072
- Bernlochner, F. U., Duell, S., Ligeti, Z., Papucci, M., & Robinson, D. J. (2020). Das ist der HAMMER: consistent new physics interpretations of semileptonic decays. The European Physical Journal C, 80(9). 10.1140/epjc/s10052-020-8304-0
- van Dyk, D., & others. (2022). EOS: a software for flavor physics phenomenology. Eur. Phys. J. C, 82(6), 569. 10.1140/epjc/s10052-022-10177-4
- Pich, A. (1998). Effective Field Theory. https://doi.org/10.48550/arXiv.hep-ph/9806303
- Heinrich, L., Feickert, M., & Stark, G. (n.d.). pyhf: v0.7.6 (0.7.6) [Computer software]. 10.5281/zenodo.1169739
- Heinrich, L., Feickert, M., Stark, G., & Cranmer, K. (2021). pyhf: pure-Python implementation of HistFactory statistical models. Journal of Open Source Software, 6(58), 2823. 10.21105/joss.02823
- Cranmer, K., Lewis, G., Moneta, L., Shibata, A., & Verkerke, W. (2012). HistFactory: A tool for creating statistical models for use with RooFit and RooStats. 10.17181/CERN-OPEN-2012-016
- García Pardiñas, J., Meloni, S., Grillo, L., Owen, P., Calvi, M., & Serra, N. (2022). RooHammerModel: interfacing the HAMMER software tool with HistFactory and RooFit. Journal of Instrumentation, 17(04), T04006. 10.1088/1748-0221/17/04/t04006
- Verkerke, W., & Kirkby, D. P. (2003). The RooFit toolkit for data modeling. eConf, C0303241, MOLT007. https://doi.org/10.48550/arXiv.physics/0306116
- Gärtner, L., Hartmann, N., Heinrich, L., Horstmann, M., Kuhr, T., Reboud, M., Stefkova, S., & van Dyk, D. (2024). Constructing model-agnostic likelihoods, a method for the reinterpretation of particle physics results. The European Physical Journal C, 84(7). 10.1140/epjc/s10052-024-13038-4
- Banerjee, Sw., Ben-Haim, E., Bernlochner, F., Bertholet, E., Bona, M., Bozek, A., Bozzi, C., Brodzicka, J., Chobanova, V., Chrzaszcz, M., Egede, U., Gersabeck, M., Goldenzweig, P., Gharbi, N., Grillo, L., Hayasaka, K., Humair, T., Johnson, D., Kuhr, T., … Yelton, J. (2024). Averages of b-hadron, c-hadron, and τ-lepton properties as of 2023. https://doi.org/10.48550/arXiv.2411.18639
- Cowan, G. A., Craik, D. C., & Needham, M. D. (2017). RapidSim: An application for the fast simulation of heavy-quark hadron decays. Computer Physics Communications, 214, 239–246. 10.1016/j.cpc.2017.01.029
- Straub, D. M. (2018). flavio: a Python package for flavour and precision phenomenology in the Standard Model and beyond. https://doi.org/10.48550/arXiv.1810.08132
