
Phlower: A Deep Learning Framework Supporting PyTorch Tensors with Physical Dimensions
Abstract¶
We present Phlower, an open-source deep learning library that extends PyTorch tensors to incorporate physical dimensions — such as time ( T ), mass ( M ), and length ( L ) — and enforces dimensional consistency throughout computations.
When applying deep learning to physical systems, tensors often represent quantities with physical dimensions. Ensuring dimensional correctness in such operations is crucial to maintaining physical validity. To address this challenge, Phlower provides PhlowerTensor, a wrapper class of PyTorch tensor that tracks physical dimensions and ensures that tensor operations comply with dimensional consistency rules.
This paper introduces the core features of Phlower and demonstrates its capability to maintain dimensional correctness through representative examples.
1Introduction¶
The simulation of physical phenomena plays a critical role in various aspects of daily life, including vehicle design and weather forecasting. As a new paradigm, physics-informed machine learning, which integrates machine learning with physical simulations, has recently gained attention, particularly with the emergence of Physics-Informed Neural Networks (PINNs) Raissi et al., 2019 and Graph Neural Networks (GNNs). Compared to traditional simulation methods, it offers the potential to accelerate predictions of physical behavior and to uncover new physical laws that might otherwise remain hidden.
As shown in Table 1, Physical dimensions are the fundamental quantities used to describe physical systems. These include time ( ), mass ( ), length ( ), electric current ( ), thermodynamic temperature ( ), amount of substance ( ), and luminous intensity ( ). In numerical simulations of physical phenomena, physical dimensions ensure the correctness of computations. Extending this concept to deep learning provides several advantages, we can enhance the reliability of model architectures by preventing invalid operations between physically incompatible quantities. This capability helps avoid subtle implementation errors and improves code readability and maintainability, especially in scientific and engineering applications where preserving physical meaning is critical.
PyTorch Paszke et al., 2019 is a deep learning framework that provides tensor operations and automatic differentiation capabilities. However, it does not natively support physical dimensions. To fill this gap, we develop Phlower, an open-source deep learning framework, and introduce PhlowerTensor, a wrapper class of PyTorch tensors and enables physical dimension tracking. This ensures that tensor operations adhere to dimensional consistency rules.
From an implementation perspective, PhlowerTensor holds an underlying PyTorch tensor, making conversion between PyTorch tensors and PhlowerTensor straightforward. Moreover, PhlowerTensor maintains compatibility with PyTorch’s autograd system and core tensor operations such as sum(), enabling seamless integration into existing PyTorch-based workflows with minimal code modifications. Program 1 illustrates its usage.
Table 1:Physical Dimensions Newell & Tiesinga, 2019
| quantity | Symbol |
|---|---|
| time | |
| mass | |
| length | |
| electric current | |
| thermodynamic temperature | |
| amount of substance | |
| luminous intensity |
from phlower import phlower_tensor
import torch
# Example: Calculating kinetic energy (E = 0.5 * m * v^2)
# A mass (m) has dimensions M^1
mass = phlower_tensor(torch.rand(10, 1), dimension={"M": 1})
# A velocity (v) has dimensions L^1 T^-1
velocity = phlower_tensor(torch.rand(10, 3, 1), dimension={"L": 1, "T": -1})
kinetic_energy = 0.5 * mass * torch.sum(velocity ** 2, axis=-1)
print(kinetic_energy.dimension)
# Output: PhlowerDimensionTensor(T: -2.0, L: 2.0, M: 1.0, I: 0.0, Theta: 0.0, N: 0.0, J: 0.0)Program 1:PhlowerTensor carrying physical dimensions
In this paper, we will introduce Phlower’s key features and demonstrate how physical dimensions are handled in deep learning workflows. The remainder of this paper is organized as follows:
Section 2 introduces the core concept of Phlower and its key features. Defining
PhlowerTensorand enforcing dimensional consistency are discussed, along with examples of tensor operations that maintain physical dimensions.Section 3 presents possible use cases of
PhlowerTensorin deep learning applications, particularly in scientific machine learning and physics-informed models. It highlights howPhlowerTensorcan prevent dimensional inconsistencies and enforce dimensional validity in feature engineering.Section 4 discusses additional features of Phlower, including YAML-based model definition and shape semantics. These features enhance the usability and flexibility of Phlower in deep learning workflows.
Section 5 compares Phlower with related work, highlighting its unique features and advantages over existing libraries for handling physical dimensions in scientific computing and machine learning.
2Core Concepts¶
2.1Design Philosophy¶
We design Phlower to extend PyTorch tensors with support for physical dimensions while maintaining full compatibility with existing PyTorch workflows.
Its design is guided by the following key principles:
Dimensional Consistency: Phlower enforces dimensional consistency during tensor operations, ensuring that operations involving tensors with incompatible physical dimensions raise informative errors. This prevents subtle bugs and improves the reliability of deep learning models.
Seamless Integration: Phlower is designed to integrate seamlessly with PyTorch, allowing users to leverage existing PyTorch functionalities while adding physical dimension tracking. This includes compatibility with PyTorch’s autograd system and core tensor operations.
Lightweight Implementation:
PhlowerTensoris implemented as a lightweight wrapper around PyTorch tensors, minimizing the overhead of using physical dimensions. This allows users to easily convert between PyTorch tensors andPhlowerTensorwithout significant performance impact.
2.2Defining PhlowerTensor¶
Program 2 shows how to create a PhlowerTensor from a PyTorch tensor. The phlower_tensor function takes a PyTorch tensor and a dictionary specifying the physical dimensions.
from phlower import phlower_tensor
import torch
# Create a PhlowerTensor with physical dimensions at each point
# Example: A tensor representing velocity with dimensions L^1 T^-1
velocity = phlower_tensor(torch.rand(10, 3), dimension={"L": 1, "T": -1})
print(velocity)
# Example: A tensor representing pressure with dimensions M^1 T^-2 L^-1
pressure = phlower_tensor(torch.rand(10, 1), dimension={"M": 1, "T": -2, "L": -1})
print(pressure)Program 2:Create PhlowerTensor from PyTorch Tensor
2.3Dimensional Consistency¶
PhlowerTensor enforces dimensional consistency during tensor operations. Program 3 demonstrates how PhlowerTensor ensures dimensional correctness when computing kinetic energy, defined as , where is mass and is velocity.
As illustrated in Figure 1, this example assumes that each point is associated with a three-dimensional velocity vector and a scalar mass. The resulting kinetic energy has dimensions , corresponding to the physical dimension of energy.
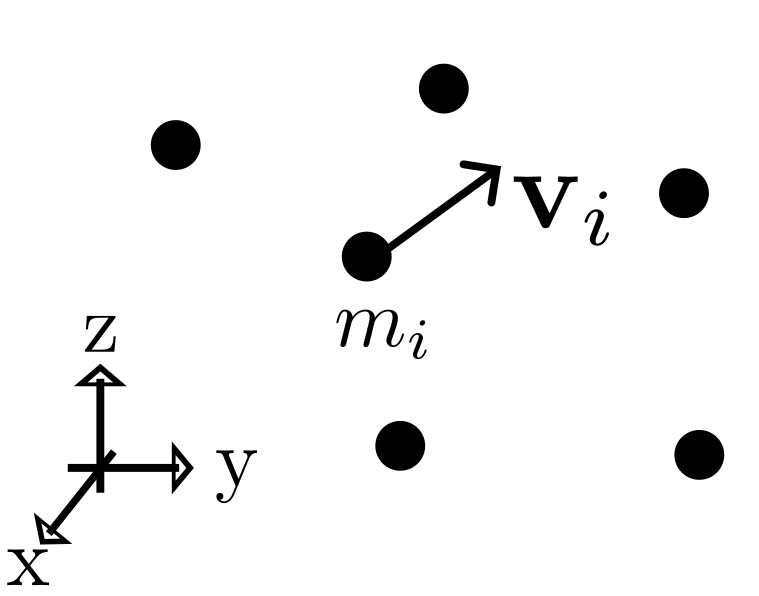
Figure 1:Example of point clouds. Each point has mass and velocity.
from phlower import phlower_tensor
import torch
# Example: Calculating kinetic energy (E = 0.5 * m * v^2)
# Mass has dimensions M^1
mass = phlower_tensor(torch.rand(10, 1), dimension={"M": 1})
# Velocity has dimensions L^1 T^-1
velocity = phlower_tensor(torch.rand(10, 3, 1), dimension={"L": 1, "T": -1})
kinetic_energy = 0.5 * mass * torch.sum(velocity ** 2, axis=-1)
print(kinetic_energy.dimension)
# Output: PhlowerDimensionTensor(T: -2.0, L: 2.0, M: 1.0, I: 0.0, Theta: 0.0, N: 0.0, J: 0.0)Program 3:Calculating kinetic energy with PhlowerTensor
On the other hand, Phlower disallows operations involving incompatible physical dimensions. Program 4 shows PhlowerTensor raise an error when attempting to add a pressure tensor to a velocity tensor.
# Example: A tensor representing velocity with dimensions L^1 T^-1
velocity = phlower_tensor(torch.rand(10, 3), dimension={"L": 1, "T": -1})
# Example: A tensor representing pressure with dimensions M^1 T^-2 L^-1
pressure = phlower_tensor(torch.rand(10, 1), dimension={"M": 1, "T": -2, "L": -1})
# Attempting to add velocity and pressure tensors with incompatible dimensions
try:
result = velocity + pressure
except ValueError as e:
print(f"Error: {e}")
# Output: Error: Add operation for different physical dimensions is not allowed.Program 4:Attempting to add tensors with incompatible dimensions
PhlowerTensor supports in-place operations (e.g., +=, *=) while enforcing dimensional consistency. Program 5 illustrates an example of in-place operations for PhlowerTensor.
# Example: In-place operation for non-dimensional tensor
# Objects other than PhlowerTensor (e.g., float) are treated as non-dimensional
non_dimensional_value = phlower_tensor(torch.rand(10, 3), dimension={})
non_dimensional_value += 5.0
# Example: A tensor representing pressure with dimensions M^1 T^-2 L^-1
pressure = phlower_tensor(torch.rand(10, 1), dimension={"M": 1, "T": -2, "L": -1})
# In-place subtraction with compatible dimensions
pressure -= phlower_tensor(torch.tensor(1.0), dimension={"M": 1, "T": -2, "L": -1})
# Attempting in-place addition with incompatible dimensions
try:
pressure += 5.0
except ValueError as e:
print(f"Error: {e}")
# Output: Error: Add operation for different physical dimensions is not allowed.Program 5:In-place operation with dimensions
2.4Array Operations¶
This section demonstrates how PhlowerTensor supports array operations while maintaining dimensional consistency.
For example, Program 6 shows that multiple velocity tensors can be stacked along a new dimension.
The resulting tensor remains PhlowerTensor with appropriate physical dimension, even though the standard torch.stack is called.
from phlower import phlower_tensor
import torch
# Example: Stacking velocity tensors with compatible dimensions
# Assuming we have multiple velocity tensors with dimensions L^1 T^-1
velocity1 = phlower_tensor(torch.rand(10, 3), dimension={"L": 1, "T": -1})
velocity2 = phlower_tensor(torch.rand(10, 3), dimension={"L": 1, "T": -1})
# Stacking along a new dimension (e.g., time)
stacked_velocity = torch.stack([velocity1, velocity2])
print(stacked_velocity.shape)
# Output: torch.Size([2, 10, 3])
print(stacked_velocity.dimension)
# Output: PhlowerTensor with dimensions L^1 T^-1 and shape (2, 10, 3)Program 6:Stacking tensors with compatible dimensions
3Use Cases¶
This section presents potential use cases of PhlowerTensor in scientific machine learning and physics-informed models. PhlowerTensor’s ability to track physical dimensions and enforce dimensional consistency makes it a valuable tool for ensuring the correctness of computations in these domains.
3.1Preventing Dimensional Inconsistencies in Physics-Informed Models¶
In physics-informed neural networks (PINNs), the loss function often includes terms derived from differential equations. For example, when modeling a system governed by Navier-Stokes equations, the loss function is composed of terms like the continuity equation and momentum equations. These equations involve physical quantities such as velocity, pressure, and density, each with specific physical dimensions. PhlowerTensor can be used to ensure that these terms are dimensionally consistent, preventing errors that could arise from mixing quantities with incompatible dimensions.
3.2Enforcing Dimensional Validity in Feature Engineering¶
Phlower can reject invalid operations in feature engineering (e.g., subtracting pressure from velocity) due to its enforcement of dimensional consistency. This capability is particularly useful in domains such as fluid dynamics (e.g., aerodynamic analysis of vehicles), where data includes a variety of physical quantities with different dimensions.
4Additional Features¶
4.1YAML-Based Definition¶
Phlower provides a YAML-based model definition system that allows users to define, configure, and reuse machine learning models efficiently. Program 7 shows an excerpt of an example YAML file. This feature simplifies experimentation by enabling users to modify model architectures and hyperparameters without changing the underlying code.
- nn_type: MLP
name: ENCODER1
input_keys:
- feature1
output_key: mlp1
destinations:
- Concat
nn_parameters:
nodes: [-1, 20, 200]
activations: ["relu", "relu"]Program 7:Example of YAML-based model definition in Phlower
4.2Shape Semantics¶
Each index in the shape of a PhlowerTensor carries semantic meaning, a concept referred to as shape semantics in Phlower. Program 8 illustrates how PhlowerTensor can represent time-series pressure using shape semantics. This positional information is crucial for ensuring that tensor operations remain semantically meaningful and consistent with the underlying physical model.
from phlower import phlower_tensor
import torch
# Example: PhlowerTensor representing pressure.
# Here, we assume that the number of time steps is 10, the number of spatial points is 100.
time_series_pressure = phlower_tensor(
torch.rand(10, 100, 1),
dimension={"M": 1, "T": -2, "L": -1},
is_time_series=True,
)
print(time_series_pressure.is_time_series)
# Output: True
print(time_series_pressure.n_vertices())
# Output: 100
# Accessing the last time step of the time series
pressure_at_last_time_step = time_series_pressure[-1]
# Phlower automatically detects that accessed tensor is not a time series
print(pressure_at_last_time_step.is_time_series)
# Output: FalseProgram 8:Shape Semantics in PhlowerTensor
4.3Output of model structure¶
Phlower provides a feature to export the model structure in a Mermaid diagram format, making it easier to integrate them into documentation. Figure 2 shows an example of model architecture diagram. This feature is useful for visualizing model structure and understanding the relationships between different components.
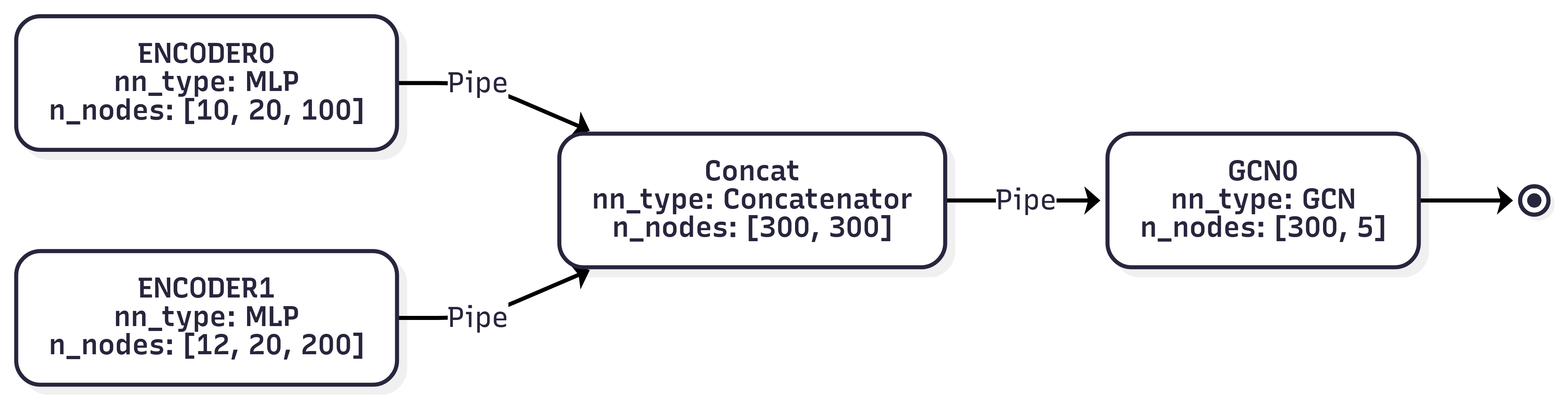
Figure 2:Example of a model structure diagram generated by Phlower.
5Related Work¶
Several libraries and frameworks have been developed to support physical dimensions in scientific computing.
Pint Grecco, 2025: A Python library for handling physical quantities with units. It allows users to define quantities such as
5 metersor25 degrees Celsius, and supports conversions between different unit systems, e.g., from meters to feet or from Celsius to Fahrenheit. Pint providesQuantityobjects that encapsulate both the numeric value and its unit, and supports NumPy-like operations while preserving unit consistency.Python Quantities Dale, 2025: A library that extends NumPy to support physical quantities with units. It enables dimensional analysis and unit conversions in scientific computations.
Python Quantitiesis designed to be compatible with NumPy arrays, allowing seamless integration with NumPy operations.
In contrast to Pint or Python Quantities, Phlower has two key differences. First, it does not provide unit conversion functionalities; instead, it focuses on enforcing dimensional consistency in tensor operations. Second, PhlowerTensor represents physical dimensions as an exponent vector of physical quantities (such as mass, length, and time) and stores this metadata alongside a PyTorch tensor. This design enables seamless integration with PyTorch, supporting GPU acceleration and automatic differentiation while tracking and validating the physical dimensions of tensor computations.
Thus, while Pint and Python Quantities aim to provide general-purpose unit handling and conversions in scientific computing built on NumPy, Phlower is specifically designed to integrate dimension checking into deep learning workflows built on PyTorch.
6Limitations¶
Runtime Overhead: Dimensional consistency is enforced at runtime, which introduces additional computational overhead. This may impact performance in scenarios where a large numbers of tensor operations are performed, particularly in real-time applications.
Partial Compatibility with PyTorch: Although
PhlowerTensoris designed to integrate with PyTorch, certain advanced features such as in-place operations or custom autograd functions may require manual adaptation or may not be fully supported.
7Conclusion and Future Work¶
In traditional numerical simulations of physical phenomena, physical dimensions play a critical role in ensuring the correctness of computations. To bring this advantage into deep learning, Phlower integrates physical dimensional information into PyTorch tensor objects. By enforcing dimensional consistency, Phlower enables users to avoid errors and improve the reliability of their deep learning models. We believe that Phlower will serve as a valuable tool for researchers and engineers working at the intersection of deep learning and physical simulation.
Future work includes extending the library to support more complex physical models and enhancing the YAML-based model definition system.
Copyright © 2025 Sakamoto. This is an open-access article distributed under the terms of the Creative Commons Attribution 4.0 International license, which enables reusers to distribute, remix, adapt, and build upon the material in any medium or format, so long as attribution is given to the creator.
- GNN
- Graph Neural Network
- PINN
- Physics-Informed Neural Network
- Raissi, M., Perdikaris, P., & Karniadakis, G. E. (2019). Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. Journal of Computational Physics, 378, 686–707. https://doi.org/10.1016/j.jcp.2018.10.045
- Paszke, A., Gross, S., Massa, F., Lerer, A., Bradbury, J., Chanan, G., Killeen, T., Lin, Z., Gimelshein, N., Antiga, L., Desmaison, A., Kopf, A., Yang, E., DeVito, Z., Raison, M., Tejani, A., Chilamkurthy, S., Steiner, B., Fang, L., … Chintala, S. (2019). PyTorch: An Imperative Style, High-Performance Deep Learning Library. In H. Wallach, H. Larochelle, A. Beygelzimer, F. d’Alché Buc, E. Fox, & R. Garnett (Eds.), Advances in Neural Information Processing Systems (Vol. 32). Curran Associates, Inc. https://doi.org/10.48550/arXiv.1912.01703
- Newell, D., & Tiesinga, E. (2019). The International System of Units (SI), 2019 Edition (Special Publication (NIST SP) No. 330–2019). National Institute of Standards. https://doi.org/10.6028/NIST.SP.330-2019
- Grecco, H. E. (2025). Pint: Physical quantities package. https://github.com/hgrecco/pint
- Dale, D. (2025). Python Quantities: Support for physical quantities with units, based on NumPy. https://github.com/python-quantities/python-quantities
